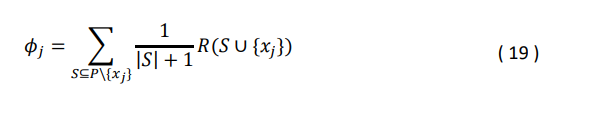Друзья, недавно натолкнулся на интересную научную статью, перевод которой представлен ниже. Исходник статьи вы можете найти по ссылке.
В этой статье рассматривается метод значений Шепли для анализа атрибуции в области интернет-рекламы. Будучи подходящим решением для распределения заслуг в теории кооперативных игр, метод значений Шепли напрямую количественно оценивает вклад входных данных интернет-рекламы в ключевой показатель эффективности (KPI) рекламы по нескольким каналам. Мы упрощаем метод расчета, разрабатывая альтернативную математическую формулу. Новая формула значительно повышает эффективность вычислений и, следовательно, расширяет область применения. На основе упрощенной формулы мы далее разрабатываем метод упорядоченных значений Шепли. Предложенный метод учитывает порядок посещения каналов пользователями. Мы утверждаем, что он обеспечивает более полное понимание, оценивая атрибуцию каналов на различных этапах пути конверсии пользователей. Предложенные подходы иллюстрируются на примерах реальных кампаний интернет-рекламы.
Ключевые слова: Теория кооперативных игр; Цифровая реклама; Моделирование атрибуции с несколькими касаниями; Метод упорядоченных значений Шепли.
1 Введение
В эпоху цифровых технологий реклама может достигать и влиять на пользователей через различные каналы и устройства. Онлайн-каналы, включая поисковые системы, паблишеры, цифровые видео и т.д., широко используются при планировании рекламных кампаний. Они воспроизводят рекламные впечатления целевым пользователям на ПК, смартфонах, планшетах и т.д. В результате решение пользователя о совершении покупки (приобретение товара или подписка на услугу) обычно вызвано множественными контактами с рекламой. Поэтому критической проблемой, интересующей рекламодателей, является вопрос о том, как ключевой показатель эффективности рекламы (KPI), такой как конверсия или доход, должен быть приписан всем рекламным каналам, участвующим в кампании. Систематические подходы к решению этой проблемы классифицируются как моделирование атрибуции.
Маркетологи начинают анализ атрибуции с простых моделей, основанных на таких правилах, как модели последнего касания (первого касания), линейные, U-образные и модели временного убывания. Они распределяют “вклады” согласно предопределенным эвристическим правилам. Однако эти модели имеют значительные ограничения. В таком случае, желаемая модель атрибуции должна быть основана на конкретных данных. Результативное распределение вложений должно быть специфичным для каждой кампании, рекламируемого продукта/услуги и даже пользователей, участвующих в кампании.
Альтернативный способ решения проблемы атрибуции основан на передовых методологиях анализа данных, известных как алгоритмические подходы, которые привлекают все больше внимания в последнее десятилетие . Шао и Ли предложили «простую вероятностную модель». Эта методология изучает, помимо эффекта каждого отдельного канала, совместное воздействие всех возможных комбинаций двух, трех или более каналов. Авторы предполагают, что на практике вклады от взаимодействий выше второго порядка можно не учитывать. Впоследствии Далессандро и др. разработали метод атрибуции важности канала как обобщение работы Шао и Ли. Этот метод анализирует взаимодействия каналов до полного порядка, то есть совместные эффекты всех рекламных каналов. Полученный подход эквивалентен методу значений Шепли в теории кооперативных игр.
Метод значений Шепли является общим подходом к распределению вложений/заслуг в теории кооперативных игр. Он основан на оценке предельного вклада каждого игрока в игру. Заслуга, присваиваемая каждому отдельному игроку, то есть значение Шепли, является ожидаемым значением этого предельного вклада по всем возможным перестановкам игроков. Метод значений Шепли нашел применение в различных областях . Например, Ма и др. применили его для разработки механизма распределения прибыли для поставщиков интернет-услуг (ISP) в интернет-экономике. В контексте атрибуции рекламы значение Шепли рассматривает рекламную кампанию как кооперативную игру, а рекламные каналы как игроков в этой игре. Каналы сотрудничают, чтобы привлекать, влиять и конвертировать пользователей. Значение Шепли каждого канала рассчитывается на основе его вклада в ключевой показатель эффективности рекламы (KPI), который может включать индивидуальные вклады и синергию с остальными.
В данной статье мы пересматриваем метод значений Шепли для моделирования атрибуции в онлайн-рекламе. Метрики эффективности, используемые в этом подходе, обсуждаются и переосмысляются специально для рекламной сферы. На основе нашей интерпретации мы разрабатываем упрощенную формулу расчета. Новая формула математически эквивалентна общему методу значений Шепли, но имеет значительно более высокую вычислительную эффективность. Мы также предлагаем рассмотреть упорядоченный метод значений Шепли, чтобы учесть эффект порядка касания рекламных каналов. Наш новый подход может предоставить больше информации об эффективности рекламных каналов на различных этапах пути конверсии пользователей.
В разделе 2 данной статьи мы рассматриваем метод значений Шепли и обсуждаем метрики эффективности рекламы, включая измерения вклада и предельного вклада. Также описываем связанные свойства, которые обеспечивают эффективность и справедливость в распределении вкладов. Раздел 3 представляет нашу упрощенную формулу расчета, в то время как подробное математическое доказательство представлено в приложении. Далее, в разделе 4, мы предлагаем упорядоченный метод значений Шепли, включая мотивацию и механизм атрибуции. Раздел 5 демонстрирует эффективность предложенных подходов на основе реального набора данных онлайн рекламной кампании. Мы завершаем нашу работу кратким обсуждением в разделе 6.
2 Метод значений Шепли
Метод Шепли рассматривает рекламные каналы как игроков в кооперативной игре. Он напрямую измеряет вклад каналов в рекламные KPI и берет среднее всех добавленных вкладов в качестве значений атрибуции. В частности, имея широкую совокупность 𝑃, состоящую из рекламных каналов {𝑥1, 𝑥2, … , 𝑥𝑝}, мы используем функцию полезности 𝜈(𝑆) для описания вклада 𝑆, который представляет совокупность каналов. Значение Шепли может быть рассчитано с использованием следующей формулы.
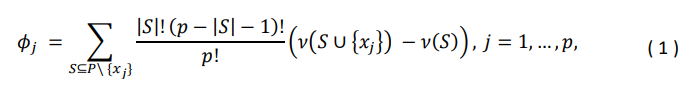
где |𝑆| — это мощность совокупности 𝑆, и сумма распространяется на все подмножества 𝑆 из 𝑃, не содержащие канал 𝑥𝑗. 𝜈(𝑆 ∪ {𝑥𝑗}) − 𝜈(𝑆), что также обозначается как 𝑀(𝑗, 𝑆), является предельным вкладом канала 𝑥𝑗 в совокупность 𝑆.
Как замечено в уравнении (1), метод Шепли принимает взвешенное среднее его предельного вклада по всем возможным совокупностям для каждого канала. Вклад совокупности и предельный вклад могут быть измерены различными способами для получения представления с разных аспектов. Это может быть связано с количеством покупок, количеством контактов, а также общим доходом (Берман, 2013). В следующих разделах мы обсудим определение вклада и предельного вклада.
2.1 Вклад
Функция полезности 𝜈(⋅) измеряет вклад совокупности каналов в рекламные KPI в отсутствие остальных. Для широкой совокупности 𝑃, которая включает все каналы кампании, 𝜈(𝑃) должно равняться общей созданной стоимости всей кампании. Стоимость кампании генерируется всеми конвертированными пользователями, которые были достигнуты рекламой. На самом деле, большинство конвертированных пользователей принимают решения после посещения определенного подмножества каналов, хотя они находятся в пределах досягаемости всех доступных каналов в 𝑃. Если мы определим 𝑢𝑗 как набор пользователей, которые посетили канал 𝑥𝑗 перед конверсией (они могли или не могли посетить другие каналы), то формула общей стоимости кампании генерируется пользователями будет:

в ней содержится все конвертированные пользователи. Эти пользователи могут быть дополнительно сгруппированы в несколько типов пользователей в зависимости от каналов, которые они посетили. Например, тип пользователя {1} содержит всех пользователей, которые конвертировались после посещения только канала 𝑥1, тип пользователя {2} содержит всех пользователей, которые конвертировались после посещения только канала 𝑥2, типы пользователей {1,2} содержат всех пользователей, которые конвертировались после посещения каналов 𝑥1 и 𝑥2, и так далее. Следовательно, мы можем определить вклад 𝑃 как

где 𝑅(𝑆) — это общая стоимость, созданная пользователями, которые посетили все каналы в 𝑆. Мы называем это индивидуальным вкладом совокупности 𝑆. Таким образом, 𝜈(𝑃) содержит вклады от всех конвертированных пользователей. Это также общая стоимость кампании и общее количество кредитов, которые должны быть распределены в нашей проблеме атрибуции.
Аналогично, для каждой совокупности 𝑆 ⊆ 𝑃, вклад 𝑆, сделанный пользователями, составляет

Это означает, что вклад любой совокупности 𝑆 измеряется как стоимость, созданная пользователями, которые конвертировались после посещения только некоторых каналов в 𝑆. Эти пользователи не должны посещать никакие каналы за пределами 𝑆. Следовательно, для любых двух совокупностей 𝑆1 и 𝑆2, удовлетворяющих условию 𝑆1 ⊆ 𝑆2, мы имеем,

Аналогично (3), мы определяем

На практике 𝑅(⋅) может быть общим числом контактов, общим числом конверсий или доходом/прибылью. В дальнейшем мы будем использовать доход в качестве нашего рекламного KPI. Наш анализ также может быть использован и в других ситуациях.
2.2 Предельный вклад
Мы количественно оцениваем дополнительный вклад канала (𝑥𝑗) при его добавлении к совокупности (𝑆) как его предельный вклад в 𝑆.
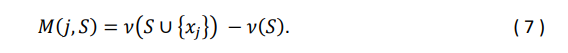
На практике это означает, что мы добавляем новый канал в существующую кампанию, которая содержит все каналы в 𝑆. Этот новый канал, вероятно, привлечет новых пользователей, которые не знают о рекламируемых продуктах или услугах. Он также может повлиять на существующих пользователей, которые уже столкнулись с некоторыми каналами в 𝑆, или конвертировать пользователей напрямую, независимо от их предыдущих контактов. С другой стороны, наличие дополнительного канала не обязательно означает, что каждый член аудитории будет продолжать находиться в цели всех существующих каналов плюс этот новый канал. Некоторые пользователи конвертируются сразу после просмотра этого нового канала, до того как другие каналы смогут достичь их. На большинство пользователей этот новый канал не подействует, потому что они конвертируются до того, как этот новый канал их коснётся.
Вклад 𝜈(𝑆 ∪ {𝑥𝑗}) создается следующими тремя типами пользователей:
- Тип 1: Пользователи, которые посетили только некоторые каналы в 𝑆.
- Тип 2: Пользователи, которые посетили только канал 𝑥𝑗.
- Тип 3: Пользователи, которые посетили канал 𝑥𝑗 И некоторые каналы в 𝑆.
Пользователи типа 1 вносят вклад в 𝜈(𝑆), который является частью 𝜈(𝑆 ∪ {𝑥𝑗}) и в конечном итоге частью 𝜈(𝑃). Пользователи типа 2 вносят вклад в 𝑀(𝑗, 𝑆), то есть индивидуальный вклад от канала 𝑥𝑗. Наконец, пользователи типа 3 также вносят вклад в 𝑀(𝑗, 𝑆), который рассматривается как рекламная синергия между 𝑥𝑗 и каналами в 𝑆.
Отметим, что предельный вклад создается дополнительными пользователями (типы 2 и 3). Следовательно, 𝑀(𝑗, 𝑆) всегда должен быть неотрицательным.
2.3 Свойства
Четкий подход значения Шепли должен иметь определенные желаемые свойства , такие как симметрия и т. д. Можно смело заявить, что наш метод, определенный выше, удовлетворяет всем этим свойствам.
- Эффективность

Это гарантирует, что сумма значений Шепли (значения атрибуции) каналов равна общей стоимости кампании. Более того, метод Шепли — это механизм, используемый для распределения общей стоимости между всеми участниками, внесшими вклад. Следовательно, мы должны обеспечить, чтобы каждый конкретный вклад (значение Шепли) происходил из общей стоимости. - Псевдоигрок: Если канал 𝑥𝑗 таков, что 𝑀(𝑗, 𝑆) = 0 для каждой совокупности 𝑆, не содержащей 𝑥𝑗, тогда

Канал, который не вносит ничего в какую-либо совокупность, получит нулевой вклад. Поскольку такие каналы не могут улучшить совместную работу, они рассматриваются как псевдоигроки и могут быть исключены из игры. - Симметрия: Если каналы 𝑥𝑗1 и 𝑥𝑗2 таковы, что 𝑀(𝑗1, 𝑆) = 𝑀(𝑗2, 𝑆) для любой совокупности 𝑆 ∈ 𝑃\{𝑥𝑗1, 𝑥𝑗2}, тогда

Свойство симметрии гарантирует, что если два канала вносят одинаковый вклад во все возможные совокупности, они получат одинаковые значения Шепли.
Наконец, мы отмечаем, что наша спецификация метода Шепли отличается от той, что представлена в литературе. В частности, Шао и Ли предложили простую вероятностную модель. Они определили вклад совокупности 𝑆 (одного канала или пары каналов) с использованием стоимости, созданной пользователями, которые посетили все каналы, то есть дополнительно обобщили эту идею метода Шепли. Следовательно, вклад широкой совокупности 𝑃 содержит только стоимость, созданную пользователями, которые посетили все каналы в кампании. Однако наш опыт работы с реальными данными показывает, что пользователи обычно не посещают все доступные каналы перед конверсией. Согласно свойству эффективности, их определение может потенциально привести к анализу, который сосредоточен только на небольшой части общей стоимости кампании. Кроме того, они интерпретировали, что предельный вклад канала, 𝑀(𝑗, 𝑆), создается дополнительными воздействиями на канал 𝑥𝑗 (после воздействий от 𝑆). Таким образом, предельный вклад может быть отрицательным, поскольку сравниваемые группы пользователей не имеют желаемого свойства включения, как в (5); то есть альтернативная группа пользователей с воздействиями на дополнительный канал не обязательно создает более высокую стоимость.
3 Упрощенный метод Шепли
Метод, который мы описали в предыдущем разделе, является прямой реализацией общего метода Шепли. Он страдает от большой вычислительной нагрузки, так как нам необходимо перебирать все возможные совокупности для каждого канала. Например, при наличии 20 каналов в кампании общее количество подсовокупностей составляет 1,048,576. Таким образом, реализация оригинальной формулы неосуществима для анализа данных в больших масштабах или для своевременной оценки эффективности рекламы. Поэтому мы разработали упрощенную формулу для расчета значения Шепли. Новая версия может рассматриваться как настраиваемая вариация общего метода Шепли для моделирования атрибуции в рекламе.
Вспомним, что мы определили несколько типов пользователей в зависимости от каналов, которые они посетили. Другими словами, для каждой совокупности 𝑆 мы находим всех пользователей, которые посетили все каналы в 𝑆 перед конверсией. Мы используем 𝑅(𝑆) для обозначения общей стоимости, созданной этими пользователями.
Как обсуждалось в разделе 2.2, предельный вклад, 𝑀(𝑗, 𝑆), создается пользователями, которые посетили канал 𝑥𝑗 плюс подмножество 𝑆 (включая пустое множество). Это мотивирует нас переписать предельный вклад следующим образом:
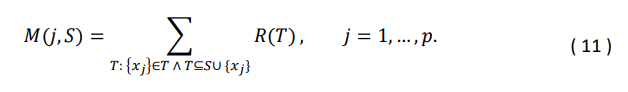
Заменив предельный вклад в (1) на (11), значение Шепли для любого канала 𝑥𝑗 просто является взвешенным средним 𝑅(𝑇) для всех возможных совокупностей 𝑇, которые содержат канал 𝑥𝑗. Вес для каждой 𝑇 рассчитывается на основе следующего упрощения:
Теорема 1: Значения Шепли в кооперативной игре, определенной в разделе 2, могут быть рассчитаны с использованием следующей упрощенной формулы:
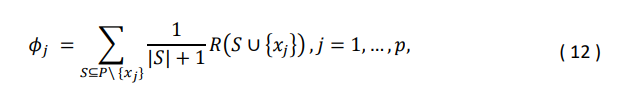
где 𝑅(𝑆 ∪ {𝑥𝑗}) обозначает доход от пользователей, которые посетили все каналы в совокупности 𝑆 ∪ {𝑥𝑗}.
Например, для канала 𝑥1 в кампании с 𝑃 = {𝑥1, 𝑥2, 𝑥3}, значение Шепли будет следующим:
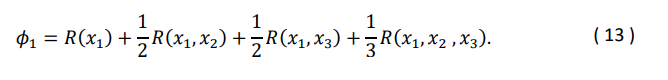
Подробное математическое доказательство представлено в приложении.
Очевидное преимущество новой формулы заключается в значительном повышении вычислительной эффективности. Вместо того, чтобы перебирать все возможные совокупности для каждого канала для расчета его предельного вклада, мы оцениваем каждую совокупность не более одного раза для каждого канала, чтобы напрямую рассчитать его значение Шепли.
Кроме более высокой вычислительной мощности, новая формула также помогает лучше понять сам метод Шепли следующим образом:
- Взаимосвязь между значениями Шепли и индивидуальным вкладом каждой совокупности (𝑅(⋅)) становится более очевидной: значение Шепли любого канала является взвешенным средним индивидуального вклада всех совокупностей, включая этот канал, и не принимает в расчет вклад от совокупностей, его не включающих.
- Мы можем легко проверить, что значения Шепли суммируются в общий результат кампании. Индивидуальный вклад каждой подсовокупности равномерно распределяется между всеми каналами, включенными в эту подсовокупность. Следовательно, сумма значений Шепли равна сумме индивидуальных вкладов всех возможных подсовокупностей, что точно соответствует общей стоимости кампании (см. (3)).
- Индивидуальный вклад любого отдельного канала 𝑥𝑗 полностью распределяется на 𝜙𝑗. Это потому, что вес 𝑅(𝑥𝑗) равен 1 в 𝜙𝑗 и 0 в 𝜙𝑘 для любого 𝑘 ≠ 𝑗.
- Если предельный вклад канала 𝑥𝑗 в каждую совокупность равен 0, как 𝑅(𝑆 ∪ {𝑥𝑗}) = 0 для каждой 𝑆, не содержащей 𝑥𝑗. Следовательно, 𝜙𝑗 также равно 0.
- Если любые два канала 𝑥𝑗1 и 𝑥𝑗2 удовлетворяют условию 𝑀(𝑗1, 𝑆) = 𝑀(𝑗2, 𝑆) для каждой 𝑆, не содержащей 𝑥𝑗1 и 𝑥𝑗2, мы имеем 𝑅(𝑆 ∪ {𝑥𝑗1}) = 𝑅(𝑆 ∪ {𝑥𝑗2}) для всех таких 𝑆. Следовательно, 𝜙𝑗1 = 𝜙𝑗2.
4 Метод упорядоченного значения Шепли
Основываясь на упрощенной формуле из раздела 3, мы дополнительно расширяем метод Шепли, включая в него эффект порядка посещения каналов пользователями. Мы называем полученный подход методом упорядоченного значения Шепли.
4.1 Мотивация
Основная проблема общего метода Шепли заключается в игнорировании конкретных путей, которые пользователи могут выбирать для достижения конверсий. Он равнодушно относится к каналам, независимо от их порядка появления в пути конверсии. Считается, что любой канал имеет такую же ценность атрибуции, как и первый или последний канал, достигший пользователя.
Однако маркетологи склонны считать, что канал может играть разные роли на разных этапах процесса конверсии. На ранних этапах кампании большинство пользователей не знают о рекламируемых продуктах или услугах. Первые несколько касаний привлекут первое внимание пользователей. Затем некоторые пользователи могут начать следить за информацией о бренде, продуктах или услугах. Далее мы активируем интересы пользователей, отправляя им рекламу через множество устройств и каналов. Наконец, некоторые пользователи принимают решения о покупке на этапе конверсии.
На практике канал может оказывать различное влияние на процесс принятия решений пользователями на разных этапах пути конверсии. Например, канал медийной рекламы обычно не содержит очень подробной информации о продуктах или услугах. Он может быть очень эффективным в качестве первого контакта. Однако он менее вероятно напрямую убедит пользователей в конверсии. Напротив, официальный сайт рекламодателя может предоставить пользователям подробную информацию и эффективнее их убедить, но может не иметь возможности достичь большого количества пользователей на ранних этапах кампании. Поэтому было бы полезно, если бы мы могли понять роль, которую каждый канал играет на каждом этапе процесса конверсии, и оценить соответствующие значения атрибуции.
4.2 Значения атрибуции
Для каждого канала 𝑥𝑗 и совокупности 𝑆 ∈ 𝑃\{𝑥𝑗}, пользователи, которые вносят вклад в 𝑅(𝑆 ∪ {𝑥𝑗}), могут посещать каналы в 𝑆 ∪ {𝑥𝑗} в различном порядке. Мы дополнительно различаем их на основе расположения канала 𝑥𝑗 в последовательности (точке контакта). В частности, мы используем 𝑅𝑖(𝑆 ∪ {𝑥𝑗}) для обозначения вклада, сделанного пользователями, которые посетили все каналы в 𝑆 ∪ {𝑥𝑗}, а также канал 𝑥𝑗 как 𝑖-й в ходе их пути конверсии. Здесь 𝑖 — это индекс для различных точек контакта в последовательности каналов. Он может принимать значения от 1, 2, … , 𝑁, где 𝑁 — это самый длинный путь конверсии для любого пользователя. Следовательно,
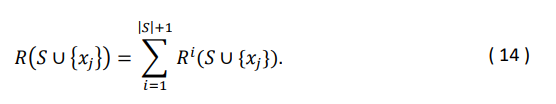
Следует отметить, что в случае, если пользователь посетил канал по нескольким точкам контакта, мы равномерно распределяем вклад по всем точкам.
Далее мы рассчитываем методом упорядоченного значения Шепли: исходя из кооперативной игры, как это определено в разделе 2, упорядоченные значения Шепли могут быть рассчитаны следующим образом:
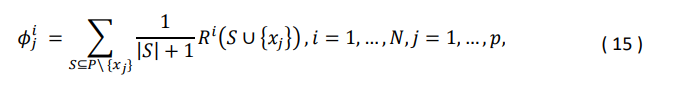
Кроме того, мы определяем следующее:
- Значение Шепли для каналов
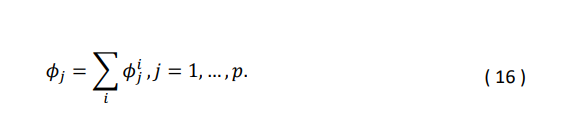
Можно увидеть, что это эквивалентно оригинальному методу Шепли, о котором говорилось в разделе 2. - Значение Шепли для точек контакта
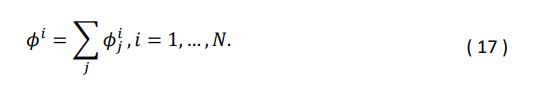
Эта формула раскрывает новые представления о том, как рекламные действия влияют на процесс принятия решений пользователями на каждом этапе их пути к конверсии.
5 Числовые результаты
В этом разделе мы используем реальный набор данных рекламной кампании для иллюстрации и демонстрации эффективности предложенных подходов.
5.1 Описание данных
Наш набор данных основан на 3-месячной онлайн-кампании, которая включает 18 рекламных каналов из 3 категорий. А именно, это паблишеры(Publishers), платформы для автоматизированных закупок рекламы (DSPs) и платный поиск (Paid Search). Набор данных содержит историю показов и конверсий каждого конвертированного пользователя. Он включает в себя всего 153,814 наблюдений, генерирующих доход. Таблица 1 представляет подробное описание набора данных.
Таблица 1: Набор данных
| Паблишеры | DSP’S | Paid search | Всего | |
| Общая выручка ($) | 2182200.57 | 6150287.95 | 6759791.57 | 14313505.32 |
| Показы | 101900 | 851333 | 97408 | 1050641 |
5.2 Анализ по группам
В этом разделе мы оцениваем эффективность трех рекламных категорий в кампании. Упомянутые методы, включая оригинальный, упрощенный и упорядоченный методы Шепли, используются для расчета значений атрибуции. Следует отметить, что значения атрибуции, приведенные в остальной части этой статьи, представлены в процентах.
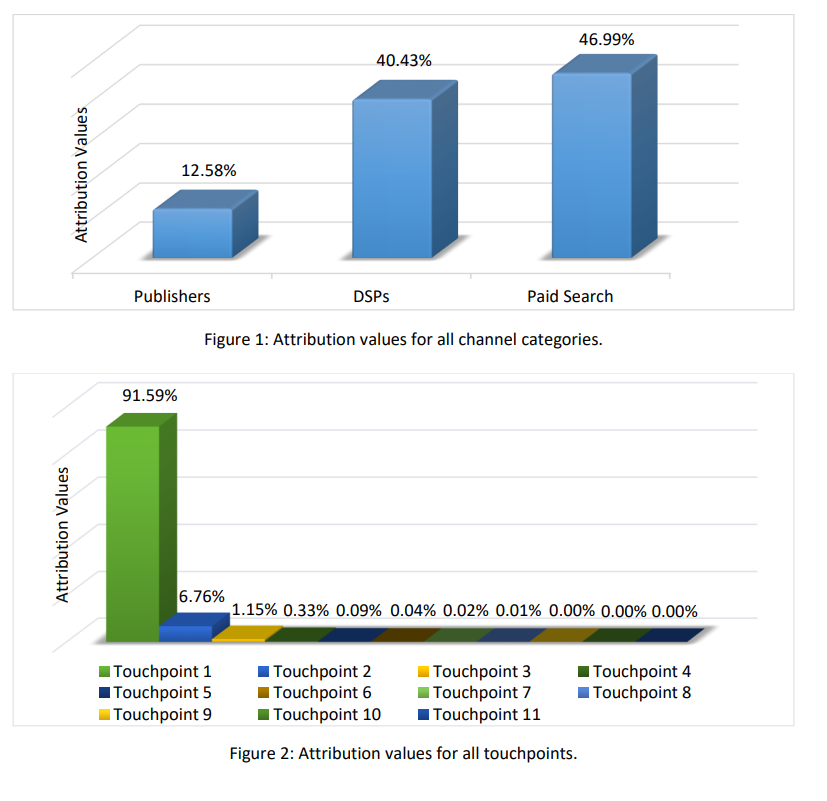
На рисунке 1 показаны значения атрибуции, полученные с помощью метода Шепли для всех категорий. Поскольку две версии формулы дают схожие числовые результаты, мы приводим только один набор значений атрибуции. Однако они существенно различаются по вычислительной эффективности: время анализа сокращается с 17 часов до примерно 2 минут на обычном ПК при использовании нашей упрощенной формулы. Как видно на диаграмме, предполагается, что категория платного поиска имеет наивысшую атрибутивную стоимость — 47%. Категории DSP присваивается несколько ниже, но очень близкая атрибутивная стоимость (40,43%). Наконец, паблишеры имеют наименьшую стоимость — 12,58%.
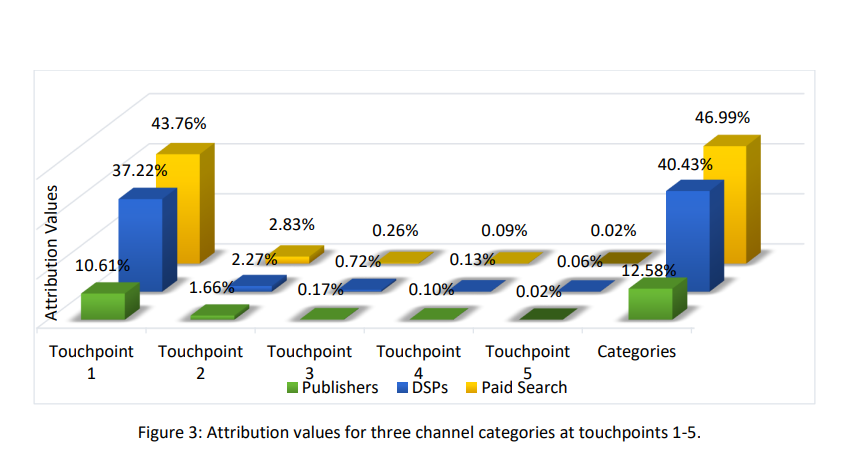
Далее мы применяем наш предложенный метод упорядоченного значения Шепли для исследования значений атрибуции различных точек контакта в процессе конверсии пользователей. В частности, значения атрибуции для всех точек контакта рассчитываются с использованием уравнения (17) и отображаются на рисунке 2. Самый длинный путь конверсии в текущем наборе данных состоит из 11 точек контакта. Как показано на рисунке 3, первая точка контакта получает большую часть кредитов (91,59%), и значение атрибуции очень быстро снижается по мере того, как пользователи посещают больше каналов. На рисунке 3 мы дополнительно представляем разбивку атрибуции по категориям каналов на точках контакта 1-5, поскольку значение атрибуции становится незначительным после пятой точки контакта. Для каждой категории первая точка контакта всегда получает наибольшее количество кредитов, а значения атрибуции остальных точек контакта довольно низкие. Однако мы замечаем, что ранжирование категорий меняется на разных этапах пути конверсии пользователей. На раннем этапе (точки контакта 1 и 2) наибольший вклад вносит платный поиск, за ним следуют DSP и паблишеры. Затем, на точках контакта 3-5, DSP играют более важную роль в дальнейшем воздействии на пользователей, которые уже имели некоторые первоначальные контакты. Отмечаем, что общие значения атрибуции для категорий каналов согласуются с общими значениями Шепли на рисунке 1. Числовые результаты также приведены в таблице 2.
Таблица 2: Значения атрибуции для трех категорий каналов на всех точках контакта.
| Точка касания | Паблишеры | DSP’S | PAID SEARCH | Общий |
| Точка касания 1 | 10.606% | 37.217% | 43.763% | 91.59% |
| Точка касания 2 | 1.658% | 2.270% | 2.835% | 6.76% |
| Точка касания 3 | 0.166% | 0.718% | 0.265% | 1.15% |
| Точка касания 4 | 0.105% | 0.133% | 0.093% | 0.33% |
| Точка касания 5 | 0.020% | 0.058% | 0.016% | 0.09% |
| Точка касания 6 | 0.016% | 0.017% | 0.007% | 0.04% |
| Точка касания 7 | 0.006% | 0.010% | 0.004% | 0.02% |
| Точка касания 8 | 0.004% | 0.005% | 0.001% | 0.01% |
| Точка касания 9 | 0.001% | 0.002% | 0.001% | 0.000% |
| Точка касания 10 | 0.001% | 0.001% | 0.000% | 0.000% |
| Точка касания 11 | 0.000% | 0.000% | 0.000% | 0.000% |
| Всего | 12.583% | 40.432% | 46.985% | 100.00% |
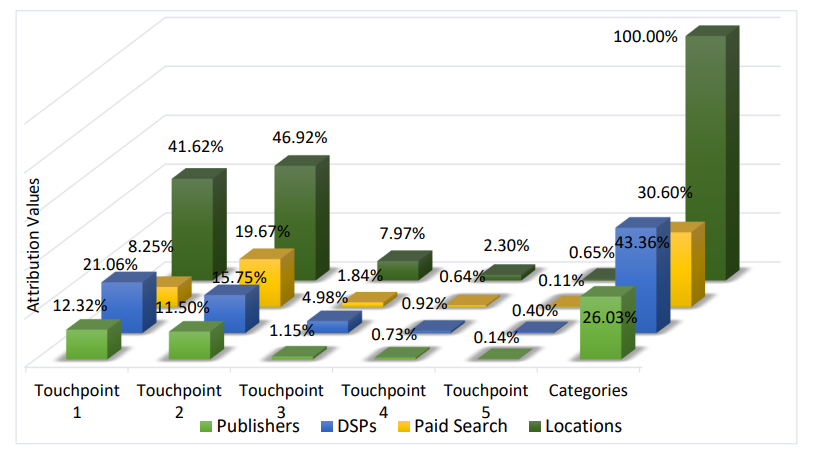
Учитывая приведенные выше числовые результаты, может возникнуть вопрос: если точка контакта 1 получает более 90% общего кредита, означает ли это, что модель первого касания подходит хорошо? Однако мы находим противоречие с общим смыслом в присвоении наивысшей атрибутивной стоимости платному поиску на ранних этапах кампании. Чтобы исследовать этот вопрос, мы дополнительно анализируем атрибуцию на основе сегментов населения. В частности, мы применяем метод упорядоченного значения Шепли к двум подгруппам пользователей. Первая группа получена путем исключения тех, кто конвертируется после посещения только одного канала. Полученные значения атрибуции отображены на рисунке 4. Важное наблюдение здесь заключается в том, что атрибутивная стоимость платного поиска на точке контакта 1 резко падает с 43,76% до 8,25%, в то время как значения атрибуции других точек контакта (особенно точки контакта 2) значительно увеличиваются. Это подразумевает, что кредит, выделенный платному поиску на точке контакта 1 (как на рисунке 3), в основном исходит от пользователей, которые конвертируются после посещения только канала платного поиска.
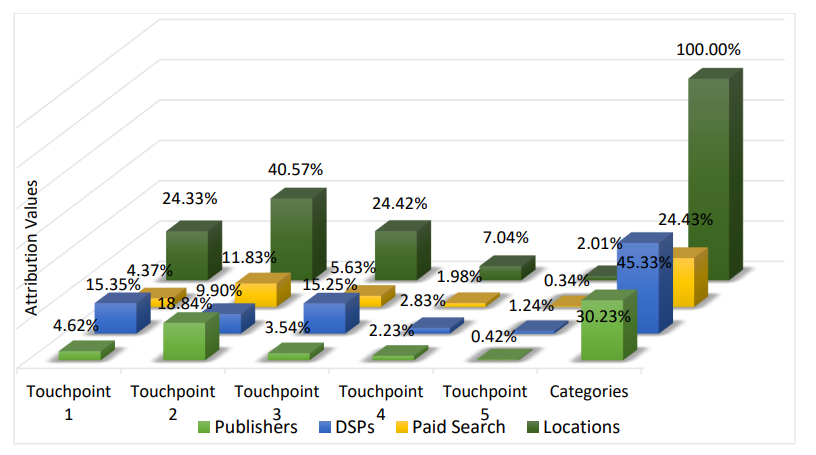
Вторая группа включает пользователей, чьи пути конверсии содержат более двух каналов. Другими словами, мы исключаем пользователей, которые конвертируются после посещения двух каналов. Результаты показаны на рисунке 5, где мы наблюдаем, что атрибутивная стоимость платного поиска на точке контакта 1 дополнительно падает до 4,37%, а значения атрибуции точек контакта 3-5, а также всех каналов на этих точках контакта продолжают увеличиваться. Более того, по сравнению с рисунком 4, значения атрибуции точек контакта 1 и 2 обе уменьшаются. Следовательно, можно сделать вывод, что определенная часть их кредитов исходит от пользователей, которые конвертируются после посещения ровно двух каналов.
На практике мы можем называть пользователей, которым требуется очень мало рекламных показов для конверсии, лояльными пользователями. В текущем наборе данных значительное количество пользователей проявляет лояльность. Некоторые пользователи даже конвертируются после посещения одного канала платного поиска. Также вероятно, что эти пользователи были подвергнуты воздействию некоторых офлайн-каналов до начала онлайн-кампании. Таким образом, они начинают свои онлайн-пути с довольно сильным желанием конвертироваться. Поскольку в настоящее время у нас нет соответствующих данных, большая часть кредитов офлайн-каналов распределяется на первый онлайн-канал, который эти пользователи обычно посещают, что в этом наборе данных в основном является платным поиском. Помимо наблюдаемой лояльности, мы видим на рисунке 5, что более 75% общих кредитов распределяются между паблишерами и DSP, которые играют важную роль на всех точках контакта. Напротив, каналы платного поиска обычно вносят умеренный вклад в доход и получают атрибутивную стоимость 24,43%.
5.3 Анализ всех каналов
В этом разделе мы оцениваем значения атрибуции для всех 18 каналов. Поскольку предложенный метод упорядоченного значения Шепли способен давать такие же результаты, как и общие значения Шепли (используя уравнение (16)), мы сосредоточимся только на нашем новом подходе. Каналы обозначены как P1, P2 и т.д. для тех, что относятся к паблишерам, D1 для канала от DSP и S1 и S2 для каналов от платного поиска.
В таблице 3 мы представляем значения атрибуции, специфичные для точек контакта, для всех каналов, а также общие значения атрибуции для каналов и точек контакта, рассчитанные с использованием уравнений (16) и (17) соответственно. Аналогично, мы сообщаем результаты только первых 5 точек контакта. Время анализа занимает около 2 минут на обычном ПК. Числовые результаты показывают, что D1 последовательно является наиболее важным участником на каждой точке контакта, за ним следуют S1 и S2. Напротив, значения атрибуции большинства паблишеров менее 1%, что является незначительным.
Таблица 4 показывает значения атрибуции на основе пользователей, которые посещают более двух каналов перед конверсией. Как видно из таблицы, D1 снова получает наивысшую атрибутивную стоимость (по-прежнему около 40%), в то время как оба канала платного поиска получают меньше кредитов. Это связано с тем, что лояльные пользователи в основном начинают свои онлайн-пути с поисковых систем. Следовательно, кредиты за рекламные усилия до кампании, которые помогают наращивать лояльность, в основном распределяются между S1 и S2. После удаления некоторых лояльных пользователей мы наблюдаем, что все паблишеры получают более высокие значения атрибуции. Предполагается, что каналы, включая P9 и P12, имеют близкие значения атрибуции к S2. Кроме того, в отличие от монотонного снижения, как в таблице 3, значения атрибуции в таблице 4 колеблются вдоль пути конверсии пользователей.
Таблица 3: Значения атрибуции для всех каналов на точках контакта 1-5.
|
Канал |
Точка контакта 1 |
Точка контакта 2 |
Точка контакта 3 |
Точка контакта 4 |
Точка контакта 5 |
Всего |
|
Р1 |
0.41% |
0.09% |
0.01% |
0.01% |
0.00% |
0.53% |
|
Р2 |
0.26% |
0.11% |
0.01% |
0.00% |
0.00% |
0.39% |
|
Р3 |
0.68% |
0.23% |
0.03% |
0.02% |
0.00% |
0.96% |
|
Р4 |
0.17% |
0.06% |
0.01% |
0.00% |
0.00% |
0.23% |
|
Р5 |
0.24% |
0.06% |
0.00% |
0.00% |
0.00% |
0.30% |
|
Р6 |
0.90% |
0.22% |
0.03% |
0.01% |
0.00% |
1.17% |
|
Р7 |
0.09% |
0.02% |
0.00% |
0.00% |
0.00% |
0.12% |
|
Р8 |
0.07% |
0.03% |
0.01% |
0.00% |
0.00% |
0.11% |
|
Р9 |
1.26% |
0.42% |
0.05% |
0.04% |
0.01% |
1.79% |
|
Р10 |
0.31% |
0.05% |
0.01% |
0.00% |
0.00% |
0.37% |
|
Р11 |
1.99% |
0.05% |
0.00% |
0.00% |
0.00% |
2.05% |
|
Р12 |
2.32% |
0.47% |
0.07% |
0.03% |
0.01% |
2.92% |
|
Р13 |
0.58% |
0.04% |
0.00% |
0.00% |
0.00% |
0.63% |
|
Р14 |
0.91% |
0.20% |
0.03% |
0.01% |
0.0% |
1.16% |
|
Р15 |
0.01% |
0.00% |
0.00% |
0.00% |
0.00% |
0.01% |
|
D1 |
37.19% |
2.17% |
0.74% |
0.12% |
0.06% |
40.28% |
|
S1 |
30.80% |
2.14% |
0.21% |
0.07% |
0.01% |
33.27% |
|
S2 |
12.55% |
1.00% |
0.12% |
0.04% |
0.01% |
13.72% |
|
Всего |
90.72% |
7.37% |
1.33% |
0.37% |
0.11% |
100.00% |
| Канал | Точка
контакта 1 |
Точка
контакта 2 |
Точка
контакта 3 |
Точка
контакта 4 |
Точка
контакта 5 |
Всего |
|---|---|---|---|---|---|---|
| Р1 | 0.17% | 0.84% | 0.21% | 0.15% | 0.03% | 1.43% |
| Р2 | 0.02% | 1.33% | 0.21% | 0.09% | 0.01% | 1.73% |
| Р3 | 0.28% | 2.10% | 0.49% | 0.31% | 0.04% | 3.30% |
| Р4 | 0.03% | 0.36% | 0.10% | 0.04% | 0.02% | 0.58% |
| Р5 | 0.11% | 0.55% | 0.08% | 0.05% | 0.01% | 0.82% |
| Р6 | 0.30% | 2.17% | 0.48% | 0.26% | 0.06% | 3.34% |
| Р7 | 0.08% | 0.24% | 0.05% | 0.03% | 0.01% | 0.41% |
| Р8 | 0.01% | 0.21% | 0.10% | 0.05% | 0.01% | 0.40% |
| Р9 | 0.58% | 3.82% | 1.00% | 0.68% | 0.11% | 6.39% |
| Р10 | 0.06% | 0.46% | 0.14% | 0.06% | 0.01% | 0.75% |
| Р11 | 2.78% | 0.70% | 0.06% | 0.01% | 0.00% | 3.56% |
| Р12 | 1.57% | 4.93% | 1.40% | 0.62% | 0.21% | 8.86% |
| Р13 | 0.09% | 0.14% | 0.08% | 0.02% | 0.00% | 0.34% |
| Р14 | 0.15% | 1.48% | 0.61% | 0.26% | 0.07% | 2.63% |
| Р15 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.01% |
| D1 | 14.05% | 7.59% | 13.94% | 2.34% | 1.10% | 39.63% |
| S1 | 3.15% | 8.51% | 3.01% | 1.30% | 0.36% | 17.29% |
| S2 | 1.66% | 3.54% | 2.30% | 0.79% | 0.13% | 8.53% |
| Всего | 25.07% | 38.97% | 25.17% | 7.06% | 2.09% | 100.00% |
6 Заключение и обсуждение
В данной работе мы реализовали альтернативную формулировку метода Шепли. Предложены и обсуждены показатели эффективности кампании и совокупности каналов. Методология обеспечивает такие свойства, как эффективность и справедливость. Разработанный подход распределяет общую стоимость кампании между всеми участвующими каналами. Наша упрощенная формула расчета приводит к настраиваемой вариации для анализа атрибуции в области рекламы. Полученная высокая вычислительная эффективность может значительно расширить область ее применения для анализа больших данных и многоканального анализа. Мы также предложили метод упорядоченного значения Шепли. Этот метод позволяет оценить атрибуцию рекламных вложений на различных этапах пути конверсии пользователей. Новые представления, которые предоставляет упорядоченная методология, помогают создать полную картину атрибуции рекламных KPI. Более того, метод упорядоченного значения Шепли может быть легко обобщен до подхода атрибуции, зависящего от времени, с немного большей вычислительной нагрузкой. Это достигается путем приписывания рекламных KPI к фактическим временным меткам (часы, дни и т.д.) вместо точек контакта.
Следует отметить, что анализ атрибуции, проведенный в статье, имеет определенные ограничения. Подозревается, что аномально высокая атрибутивная стоимость, присвоенная платному поиску на раннем этапе кампании, частично происходит от офлайн-каналов. Другими словами, отсутствие данных об офлайн-каналах затрудняет корректное количественное определение вклада онлайн-усилий. Следовательно, существует потребность в решении по интеграции данных, которое объединяет онлайн и офлайн каналы, что выходит за рамки текущего исследования. Тем не менее, мы частично решили эту проблему, отфильтровав некоторых «лояльных» пользователей.
Областью будущего развития является включение рекламного эффекта накопления в метод упорядоченного значения Шепли. Это позволяет учитывать такой переносимый эффект при оценке атрибутивной стоимости точек контакта. Еще одним направлением улучшения является связь методов Шепли с планированием рекламных кампаний или оптимизацией между каналами. Как обсуждалось в Ma et al. (2010), механизм Шепли естественным образом побуждает игроков в кооперативной игре принимать глобально оптимальную стратегию. Эгоистичное поведение игроков в конечном итоге приводит к максимизации стоимости всей игры. В контексте атрибуции в рекламе это означает, что рекламный план, максимизирующий общую стоимость кампании, автоматически максимизирует значение Шепли (кредиты, присвоенные) каждого канала, т.е. решение в рамках равновесия Нэша. Это можно легко проверить, используя наши выводы в этой статье (уравнения (3) и (12)). Однако следует отметить, что этот вывод справедлив только при отсутствии ограничений по бюджету. Будет полезно сочетать анализ атрибуции с прогнозирующим моделированием и разработать эффективную стратегию распределения бюджета в предложенной рамке теории игр.
Приложение
В этом разделе мы сначала представляем и доказываем лемму, за которой следует доказательство Теоремы 1.
Лемма: 𝑛 — положительное целое число. Для любого целого числа 𝑛0 из интервала [1, 𝑛], мы имеем
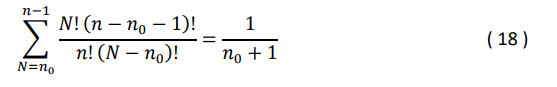
Доказательство:

Доказательство Теоремы 1:
Для любого канала 𝑥𝑗, 𝜙𝑗 является линейной комбинацией 𝑅(𝑆 ∪ {𝑥𝑗}) для 𝑆 ⊆ 𝑃\{𝑥𝑗}. Это связано с тем, что, как обсуждалось в разделе 3, каждый предельный вклад, 𝑀(𝑗, 𝑆), является суммой 𝑅(𝑆’ ∪ {𝑥𝑗}) для 𝑆’ ⊆ 𝑆.
Затем, для любой конкретной совокупности 𝑆0 ⊆ 𝑃\{𝑥𝑗} с |𝑆0| = 𝑝0, мы хотим оценить вес 𝑅(𝑆0 ∪ {𝑥𝑗}) в 𝜙𝑗. Поскольку 𝑅(𝑆0 ∪ {𝑥𝑗}) принадлежит всем возможным 𝑀(𝑗, 𝑆) с 𝑆0 ⊆ 𝑆 ⊆ 𝑃\{𝑥𝑗}, его вес просто равен сумме весов таких 𝑀(𝑗, 𝑆) в оригинальной формуле.
Следовательно, его вес равен:
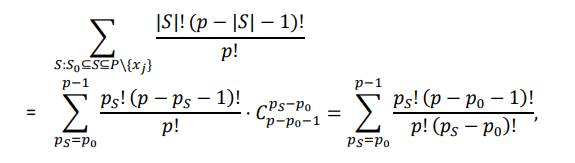
где 𝑝𝑆 обозначает мощность множества 𝑆, то есть |𝑆|. представляет собой общее количество 𝑆′, которые удовлетворяют условию 𝑆0 ⊆ 𝑆 ⊆ 𝑃\{𝑥𝑗}. Это рассчитывается путем выбора дополнительных |𝑆| − |𝑆0| = 𝑝𝑆 − 𝑝0 каналов из пула 𝑝 − |𝑆0| − |{𝑥𝑗}| = 𝑝 − 𝑝0 − 1 доступных каналов и добавления их к 𝑆0 для формирования допустимого 𝑆. Сумма распространяется на все возможные мощности 𝑆.
Согласно лемме, мы можем дополнительно упростить вышеуказанную формулу следующим образом:
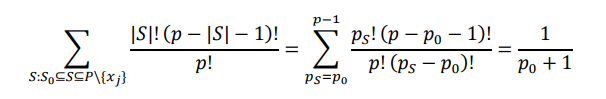
Другими словами, вес любого 𝑆0 в 𝜙𝑗 просто равен . Поскольку это верно для любого произвольного 𝑆0 ⊆ 𝑃\{𝑥𝑗}, мы получили окончательную формулу: