Моделирование атрибуции, основанной на доходах, для онлайн рекламы

Эта статья рассматривает и предлагает несколько методов моделирования атрибуции, которые позволяют количественно оценить, как доходы должны быть обусловлены входными данными рекламы. Мы адаптируем и разрабатываем метод относительной важности, основанный на регрессионных моделях, которые были широко изучены и использованы для исследования взаимосвязи между рекламными вложениями и рыночной реакцией (доходами). Метод относительной важности направлен на разложение и распределение предельных вкладов в коэффициент детерминации (𝑅2) регрессионных моделей в качестве значений атрибуции. В частности, мы адаптируем два альтернативных подхода для выполнения этой детерминации: анализ доминирования и анализ относительной нагрузки. Кроме того, мы демонстрируем расширение методов детерминации от стандартной линейной модели к аддитивной модели. Мы утверждаем, что наши новые подходы более гибки и точны в моделировании лежащих в основе отношений и расчете значений атрибуции. Мы используем примеры симуляций, чтобы продемонстрировать превосходную эффективность наших новых подходов по сравнению с традиционными методами. Мы также иллюстрируем ценность наших предложенных подходов, используя набор данных реальной рекламной кампании.

1 Введение

Доходы от цифровой рекламы в США за первую половину 2015 года составили 27,45 млрд долларов, при этом с 2005 по 2014 год наблюдался сложный годовой темп роста в 17% (IAB, 2014). Цифровая реклама позволяет маркетологам видеть полные траектории путей конверсии пользователей (т.е. последовательность и время, а также уровень вовлеченности в рекламные каналы, которые их затронули), а также получать информацию о их демографических данных, предпочтениях в покупках и многом другом. Анализируя эти данные, маркетологи могут получить более глубокие представления о том, как реклама влияет на пользователей и, соответственно, на их покупательскую активность. Эти знания, в свою очередь, помогают принимать более обоснованные решения при планировании инвестиций в рекламу.

Различные онлайн-каналы, включая поиск, баннерную рекламу, цифровое видео и т.д., используются в кампаниях цифровой рекламы. Каждый отдельный пользователь обычно подвергается воздействию комбинации каналов перед принятием решения о покупке. Поэтому фундаментальная проблема измерения эффективности и эффективности рекламы заключается в том, чтобы выяснить, как доходы должны быть распределены между группой рекламных каналов. Проблема атрибуции, изучаемая в данной работе, может быть сформулирована следующим образом. Имея последовательность записей о доходах (𝑦) и историю воздействия на пользователей 𝑝 рекламных каналов (𝑥₁, … 𝑥_𝑝), мы количественно определяем, как 𝑦 должны быть приписаны 𝑥_𝑗, и сообщаем значения атрибуции 𝜙_𝑥𝑗 для 𝑗 = 1, . . , 𝑝. Это обозначение мы используем последовательно для всех методов, обсуждаемых в данной работе.

Модели и методы атрибуции предоставляют систематические подходы к решению проблемы атрибуции. Один из распространенных методов атрибуции, используемых специалистами в отрасли, — это модель последнего (первого) касания. Она отдает все заслуги последнему (первому) каналу, с которым столкнулся конвертированный пользователь. Однако, этот подход имеет недостатки, так как он систематически недооценивает каналы, которые взаимодействуют с клиентами, находящимися дальше (ближе) по отношению к воронке конверсии.

Для лучшего распределения индивидуальных вкладов и синергии, методологии, основанные на алгоритмах, привлекают все больше внимания за последнее десятилетие некоторые авторы предложили «простую вероятностную модель». Она анализирует, помимо эффекта каждого отдельного канала, совместный эффект всех возможных комбинаций из 2, 3 или более каналов. Впоследствии Далессандро и др. разработали метод атрибуции важности канала как обобщение работы Шао и Ли. Этот метод анализирует взаимодействия каналов в четком порядке, так называемые совместные эффекты всех рекламных каналов. Полученный подход, как обсуждается в их работе, эквивалентен методу Шепли в кооперативной теории игр. Эти подходы классифицируются как прямые методы, поскольку они напрямую анализируют вклад каналов в терминах вложений (конверсия, вероятность конверсии или доход). Параллельно, регрессионные модели стали очень популярными при исследовании связи между доходом и рекламными усилиями. Методы атрибуции, включающие вспомогательную модель, такую как регрессия, считаются косвенными подходами к атрибуции, поскольку атрибуции основаны на предполагаемой (регрессионной) модели связи между рекламным воздействием и доходом. Насколько нам известно, мы находим метод относительной важности как единственный набор соответствующих регрессионных подходов для проблемы атрибуции, основанной на доходе, среди обширной статистической литературы по регрессионным моделям.

Методы определения относительной важности направлены на разложение коэффициента детерминации (R²). Это разложение осуществляется либо с помощью анализа доминирования, либо с помощью анализа относительных весов. Анализ доминирования изучает все вложенные подмодели, то есть модели, включающие подмножества переменных. Он происходит из концепции Шепли в теории кооперативных игр, чтобы измерить предельный R², добавляя каждую переменную к каждой возможной подмодели. Затем рассчитываются значения атрибуции как агрегации всех предельных эффектов. Этот анализ страдает от проблем вычислительной эффективности; количество подмоделей, которые нужно подогнать, растет экспоненциально с увеличением числа переменных. Анализ относительных весов является альтернативным подходом, разработанным Джонсоном. Этот анализ создает набор вспомогательных некоррелирующих переменных на основе сингулярного разложения. Затем он рассчитывает значения атрибуции для этих вспомогательных переменных, которые впоследствии трансформируются обратно в оригиналы. Показано, что этот анализ дает результаты, очень похожие на результаты, полученные с помощью анализа доминирования, но со значительно большей вычислительной эффективностью.

В данной работе мы реализуем несколько подходов к многоканальной атрибуции, основанных на доходах, и дополнительно разрабатываем метод относительной важности. Мы расширяем метод относительной важности от линейных регрессий до аддитивных моделей: полупараметрический тип модели. Линейная регрессионная модель неявно предполагает, что рекламные каналы вносят вклад в доход линейным образом. Поскольку это обычно ограничивающее предположение ожидать, что процесс генерации данных любого реального набора данных будет линейным, полученные значения атрибуции, скорее всего, будут неточными. Нелинейные параметрические модели, такие как логистическая регрессия, могут быть жизнеспособными альтернативами. Тем не менее, все еще сложно оправдать предположение о какой-либо предполагаемой структуре модели. Синергия между рекламными каналами может быть очень высокой и сильно варьироваться в зависимости от страны, сегмента пользователей, отрасли, продукта и многих других факторов и их комбинаций. Другими словами, хорошая модель должна обеспечивать гораздо большую гибкость в раскрытии лежащих в основе отношений. Аддитивная модель, как полупараметрическая модель, часто используется в областях эконометрики, статистики и машинного обучения для достижения степени гибкости. Хотя она все еще включает параметрический компонент, который контролирует общую модель, непараметрический компонент обеспечивает ей эту гибкость. Таким образом, полупараметрические подходы имеют потенциал быть важным вспомогательным моделирующим парадигмом для косвенных подходов к атрибуции.

Остальная часть статьи организована следующим образом. В разделе 2 мы рассматриваем и обсуждаем несколько традиционных подходов к атрибуции на основе линейной регрессионной модели. Затем мы представляем подробное описание наших предложенных методов относительной важности в разделе 3. Раздел 4 демонстрирует производительность предложенных методологий на примерах как симулированных, так и реальных данных. Мы завершаем нашу работу кратким обсуждением в разделе 5.

2 Обзор устаревших методов

Различные методы были разработаны для измерения важности переменных до появления методов относительной важности. Они в основном основаны на корреляциях между переменными и коэффициентами из стандартной линейной модели 𝑦 и 𝑿 = (𝑥₁, … 𝑥_𝑝), определенной следующим образом,

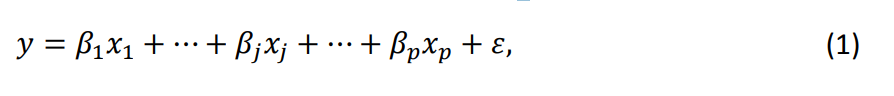
где 𝜀 — это ошибка, которая следует нормальному распределению с нулевым средним и дисперсией 𝜎^2, независимо для всех наблюдений. Без ущерба для общего мы предполагаем, что зависимая переменная 𝑦 и переменные 𝑥𝑗 стандартизированы так, чтобы иметь среднее значение 0 и дисперсию 1, так что перехват можно исключить из анализа. Мы обозначаем коэффициент детерминации этой модели как.

2.1 Коэффициенты регрессии

Коэффициенты регрессии, возможно, являются наиболее традиционными измерениями, используемыми для оценки важности переменных. Вектор 𝜷 = (𝛽₁, … , 𝛽_𝑝) представляет изменения в 𝑦, связанные с изменением каждой независимой переменной на единицу при неизменности других. В случае отсутствия взаимосвязей между переменными, 𝛽_𝑗 эквивалентен корреляции 𝑦 и 𝑥_𝑗, которая обозначается как 𝜌_𝑦,𝑥_𝑗 = 𝑐𝑜𝑟(𝑦, 𝑥_𝑗). Кроме того, мы имеем

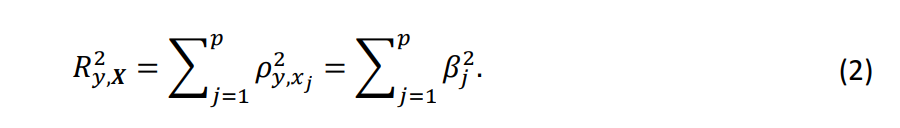
Это уравнение подразумевает, что квадраты коэффициентов (𝛽𝑗²) идеально разделяют 𝑅𝑦,𝑿² при отсутствии взаимосвязей между переменными и, следовательно, являются эффективными мерами важности переменных. Мы находим три наивные основы атрибуции, использующие этот факт: , и 𝛽_{𝑥𝑗𝜌𝑦},𝑥_𝑗, 𝑗 = 1, … , 𝑝. Как отмечено в ряде литературных источников, уравнение (2) может иметь значительные отклонения в случае ненулевой взаимосвязи между переменными. Следовательно, использование коэффициентов регрессии в качестве основ атрибуции неприемлемо, поскольку это игнорирует взаимодействия между каналами рекламы.

2.2 Квадратичные корреляции

Как упоминалось в пункте 2.1, квадрат корреляции 𝝆² = () является другой очевидной и популярной мерой важности переменных. Однако в случае ненулевой взаимосвязи ее использование еще менее предпочтительно. Это связано с тем, что она использует только корреляцию между 𝑦 и каждым отдельным 𝑥_𝑗 и, следовательно, игнорирует общие взаимоотношения переменных, которые учитываются в регрессионной модели.

2.3 Результат коэффициентов регрессии и корреляций

Имея 𝜷 и 𝝆, определенные в предыдущих разделах, можно естественно объединить их и рассмотреть произведение, 𝛽_{𝑥𝑗𝜌𝑦},𝑥_𝑗, 𝑗 = 1, … , 𝑝 . Этот метод становится трудно обосновать и реализовать, особенно когда результат в отрицательном значении.

2.4 Методы относительной важности

Методы относительной важности направлены на декомпозицию коэффициента детерминации (𝑅²) регрессионных моделей. В основном, нам нужно:
1) выбрать/подобрать регрессионную модель, которая описывает взаимосвязь доходов и усилий по рекламе;
2) декомпозировать полученный 𝑅².
В этом разделе мы представляем подробное описание предложенных подходов, включая методы декомпозиции 𝑅² (анализ доминирования и анализ относительного веса) и как мы их реализуем для наших выбранных регрессионных моделей (линейные и аддитивные модели).

3.1 Декомпозиция 𝑅2

В качестве альтернативы использованию регрессионного коэффициента и корреляции в качестве индикатора изменений в коэффициенте детерминации (𝑅²), методы относительной важности напрямую декомпозируют и распределяют 𝑅². 𝑅² регрессионной модели отражает ту часть дисперсии зависимой переменной, которую можно объяснить с помощью адаптированной модели к соответствующему подмножеству переменных. Коэффициент детерминации не может уменьшаться, когда подмножество пополняется новыми переменными. Поэтому получаемые значения атрибуции всегда неотрицательны. В этом разделе мы представляем анализ доминирования и анализ относительного веса на стандартной линейной модели, как это указано в (1).

3.2 Анализ доминирования

Анализ доминирования (DA) сравнивает коэффициенты детерминации всех вложенных подмоделей, составленных из подмножеств независимых переменных (одна ковариатная переменная исключена, удаление пар, удаление троек, группы переменных, все возможные варианты и т.д.) с полной моделью. Оценка всех подмоделей гарантирует, что взаимодействия полностью учитываются при расчете значений атрибуции. Более точно, DA проводится следующим образом:

• Рассчитайте 𝑅𝑦,𝒙₂ для каждой подмодели (из общего числа 2𝑝 − 1 подмодель). Здесь мы используем 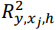для обозначения объясненной дисперсии подмоделью, которая содержит переменные с индексами в {𝑗} ∪ ℎ, где ℎ — любое подмножество {1, … , 𝑝}\{𝑗}.
• Сравните попарную относительную важность для каждой пары переменных (всего 𝑝(𝑝 1)/2 таких пар). В частности, сравните 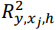и 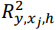при 𝑖 ≠ 𝑗, где ℎ ⊆ {1, … , 𝑝}\{𝑖,𝑗}.
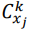• измеряет маргинальный вклад переменной 𝑥_𝑗 при добавлении к подмодели, состоящей из 𝑘 переменных, исключая 𝑥_𝑗. Существует (𝑝−1𝑘) таких подмоделей, 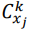рассчитывается путем усреднения связанного прироста 𝑅².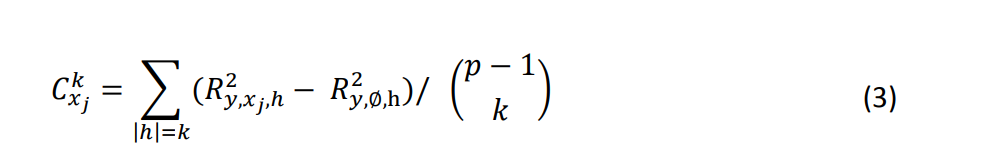
• Значение атрибуции 𝑥_𝑗, следовательно, определяется как:
• Значения атрибуции разделяют 𝑅 𝑦,𝑿²:

Мы, наконец, определяем два понятия доминирования ковариат:

• Полное доминирование: 𝑥𝑖 полностью доминирует над 𝑥𝑗, если для всех ℎ ⊆ {1, … , 𝑝}\{𝑖,𝑗}.

Общее доминирование: 𝑥_𝑖 в общем доминирует над 𝑥_𝑗, если 𝜙_𝑥𝑖 ≥ 𝜙_𝑥𝑗.
Концепции доминирования могут полноценно нарисовать полную картину для паттернов относительной важности переменных. Через анализ доминирования можно решать проблемы, такие как вопрос о том, является ли определенная группа переменных более важной, чем другая, в присутствии или отсутствии некоторых других переменных. Внутренняя проблема анализа доминирования заключается в вычислительной эффективности: для получения значений атрибуции необходимо оценить 2^𝑝 − 1 подмодель.

3.1.2 Анализ относительных весов

Как упоминалось в разделе 2.1, квадрат коэффициента регрессии является несовершенной мерой важности переменной, поскольку он не учитывает взаимные корреляции. С другой стороны, точные атрибуции очень сложно получить с помощью анализа доминирования. Идея анализа относительного веса (RW) заключается в создании нового набора ортогональных переменных из исходных, чтобы избавиться от взаимных корреляций. Таким образом, значения этих вспомогательных переменных становятся непосредственно применимыми как значения относительной важности. Более того, поскольку эти переменные являются линейными комбинациями исходных переменных, их можно легко преобразовать обратно в исходные.

Мы предполагаем, что матрица независимых переменных, состоящая из 𝑛 наблюдений, 𝑿 ∈ ℝ𝑛×𝑝, может быть разложена с использованием сингулярного разложения (SVD) следующим образом:

где столбцы 𝑷 являются собственными векторами 𝑿𝑿’. Столбцы 𝑸 содержат собственные векторы 𝑿′𝑿. 𝚫 — это диагональная матрица, содержащая сингулярные значения 𝑿. Сингулярные значения являются квадратными корнями из собственных значений 𝑿′𝑿 и 𝑿𝑿′. Таким образом, лучшее ортогональное приближение 𝑿 (то есть приближение 𝒁, которое минимизирует поэлементную сумму квадратов 𝑿 − 𝒁) может быть представлено как:

в которых столбцы 𝒁 представляют собой ортогональные векторы, которые не коррелируют друг с другом. Вектор коэффициентов при регрессии 𝒚 на ортогональные переменные 𝒁 получается как

Поскольку столбцы 𝒁 не коррелируют, 𝜷^∗𝟐 являются эффективными мерами относительной важности переменных 𝒁 для 𝒚. Затем мы проводим регрессию столбцов 𝑿 на 𝒁, чтобы получить значения важности 𝑿.

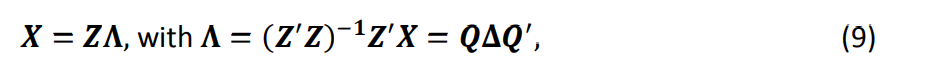
где 𝚲 — это матрица регрессионных весов 𝒁 на 𝑿. Осознав, что 𝒁 является просто линейным преобразованием 𝑿, связи между 𝜷^∗𝟐 и относительными весами переменных 𝑿 на 𝒚 могут быть восстановлены как

В итоге, у нас есть ∑_𝑗 𝜙_𝑥𝑗 = , где 𝜙_𝑥𝑗 — 𝑗-й элемент вектора 𝝓.

Одним из немедленных преимуществ анализа относительных весов является вычислительная эффективность, поскольку нет необходимости рассматривать множество подмоделей. Кроме того, анализ относительных весов и анализ доминирования обычно дают довольно схожие значения относительной важности.

3.2 Регрессионные модели

Для расчёта значений атрибуции в нашей задаче необходимо выполнить разложение 𝑅² на регрессионных моделях, которые отражают взаимосвязь между доходами и вложениями в рекламу. Однако, насколько нам известно, все существующие методы разложения 𝑅² разработаны для стандартных линейных моделей. Из-за параметрических ограничений на структуру модели линейная регрессия может не точно описывать истинную относительную важность. Чтобы улучшить возможности моделирования и увеличить гибкость, мы расширяем наш выбор регрессионных моделей в методах определения относительной важности, применяя разложение 𝑅² к полупараметрической модели.

3.2.1 Линейные модели

Как было обсуждено ранее, регрессионная модель, определенная в (1), на которой основаны методы декомпозиции 𝑅², является самой простой разновидностью линейных моделей. Однако линейная модель также относится к более широкому классу регрессионных моделей, которые линейны по коэффициентам. Другими словами, допускается нелинейное преобразование независимых переменных (таких как квадратичное, кубическое и т. д.). Полученная регрессионная модель все еще считается линейной, пока зависимая переменная представлена в виде линейной комбинации других (преобразованных) переменных. В этом смысле также стоит упомянуть, что декомпозиция 𝑅² может быть легко расширена на эти модели, обрабатывая преобразованные переменные так же, как и их неизмененные аналоги.

3.2.2 Аддитивные модели

В отличие от стандартной линейной модели, которая предполагает, что компоненты модели происходят из известных параметрических форм, аддитивная модель известна своей большей гибкостью в интеграции непараметрических компонентов модели. Она имеет следующую общую формулу:

где 𝑓_𝑗(𝒙_𝑗) — неизвестные функции, которые действуют на переменные 𝒙_𝑗 = (𝑥_1,𝑗, … , 𝑥_𝑛,𝑗), где 𝑛 — количество наблюдений, а _𝜀 — ошибка. Обратите внимание, что для функций 𝑓_𝑗 не предусмотрена специфическая функциональная формула, их предстоит оценить. Далее мы оцениваем аддитивную модель, переписывая её в линейную модель с использованием усеченного степенного сплайна (TPS), и затем применяем методы оценки относительной важности.

TPS — популярная и простая схема аппроксимации для оценки непараметрических функций. При соблюдении определенных условий непрерывности и равномерности, она может использоваться для аппроксимации функций с высокой точностью и вычислительной эффективностью. В частности, TPS аппроксимирует неизвестную функцию 𝑓_𝑗, используя линейную комбинацию следующих баз (обозначенных как 𝐵₀(𝑥), 𝐵₁(𝑥), …, 𝐵_𝑞+𝐾(𝑥)),

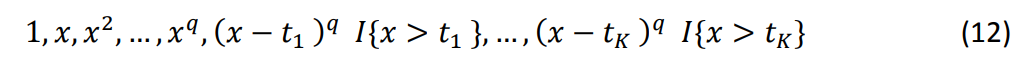
где 𝑞 — наивысший порядок полинома, обычно устанавливаемый равным 3 (кубический сплайн), и 𝑡₀ = (𝑥_𝑖) < 𝑡₁ < 𝑡₂, … , < 𝑡_𝐾 < (𝑥_𝑖) = 𝑡_𝐾+1 разбивает [ (𝑥_𝑖) , (𝑥_𝑖)] на подинтервалы [𝑡_𝑘,𝑡_𝑘+1 ), k = 0, … ,𝐾, с 𝐾 внутренними узлами. 𝐼{∙} — индикаторная функция: она принимает значение 1, если условие в скобках выполняется; иначе – 0. На практике 𝐾 является параметром настройки и настраивается с использованием кросс-валидации.
Мы выбираем равномерно расположенные узлы. Например, если (𝑥_𝑖) = 1 и (𝑥_𝑖) = 0, равномерно расположенные узлы при 𝐾 = 4 будут 0.2, 0.4, 0.6 и 0.8.
Имея четко определенные функциональные базы, мы приступаем к оценке следующего,

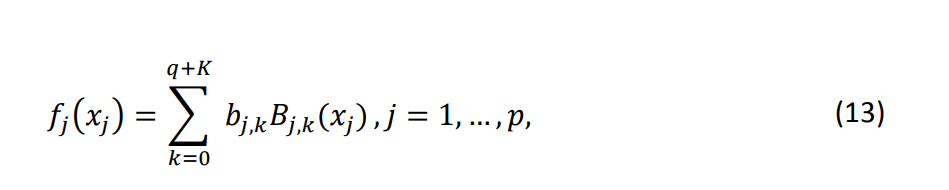
где 𝑏_𝑗,𝑘, 𝑘 = 0, … , 𝑞 + 𝐾 — коэффициенты, подлежащие оценке, и 𝐵_𝑗,𝑘(𝑥_𝑗), 𝑘 = 0, … , 𝑞 + 𝐾 обозначают базы TPS, созданные с использованием переменной 𝑥𝑗. Подставляя (13) в модель (11), мы снова получаем линейную модель, поскольку она линейна по коэффициентам (𝑏_𝑗,𝑘). Следовательно, модель может быть оценена методом наименьших квадратов.
Наконец, мы принимаем методы относительной важности, представленные в разделе 3.1 в качестве дополнения к аддитивной модели. Сначала мы рассчитываем значения относительной важности всех баз TPS, созданных с использованием каждой из исходных переменных (𝑥_𝑗), и обозначаем их как 𝜙_{𝐵𝑗,𝑘} вместе с 𝑗 = 1, . . . , 𝑝 и 𝑘 = 0, . . . , 𝑞 + 𝐾. Чтобы извлечь относительную важность 𝑥𝑗, мы выбираем сумму всех членов, зависящих от 𝑥_𝑗, значения относительной важности 𝜙_{𝐵𝑗,𝑘} с 𝑘 = 0, . . . , 𝑞 + 𝐾. То есть,

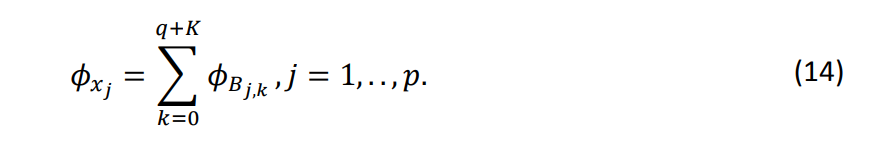
4 Численные результаты

В этом разделе мы используем различные симулированные и реальные наборы данных для демонстрации эффективности предложенных методов оценки относительной важности. К ним относятся анализ доминирования с линейными и аддитивными моделями, а также анализ относительного веса с линейными и аддитивными моделями. Сначала мы используем три симуляционных примера для иллюстрации преимуществ предложенных методов относительной важности. В примере 1 мы генерируем синтетический набор данных на основе линейной модели, чтобы подтвердить превосходную эффективность предложенных методов по сравнению с традиционными метриками. Затем в примере 2 увеличиваются корреляции (синергии) между переменными. Это используется для демонстрации того, что предложенные методы могут учитывать такую информацию и выдавать разумные значения атрибуции. Наконец, в примере 3 мы генерируем другой набор данных на основе аддитивной модели с некоторыми нелинейностями. Методы оценки относительной важности, основанные на линейных моделях, сравниваются с теми, что основаны на аддитивных моделях. Численные результаты показывают, что непараметрические функции в аддитивных моделях могут аппроксимировать различные насыщающие и ненасыщающие функции преобразования, которые очень популярны на практике в маркетинге. Значения атрибуции будут рассчитаны соответственно.

На основе реального набора данных кампании мы проводим анализ как по группам, так и по всем каналам, чтобы продемонстрировать эффективность предложенных подходов. Мы анализируем, как доходы должны быть распределены между различными категориями каналов (паблишеры против DSP против платного поиска), а также между всеми отдельными каналами, участвующими в кампании.

4.1 Пример моделирования 1: Методы относительной важности

В примере 1 мы применяем предложенные методы относительной важности к симулированному набору данных. Сгенерировано сто точек данных, (𝒙_𝑖, 𝑦_𝑖),
где 𝑖 = 1, … ,100, на основе стандартной линейной модели, как указано в (1), где 𝜷 = (3, −4.5, −0.5, 3, −4). Переменные 𝑥_𝑖,𝑗 генерируются из стандартного нормального распределения с матрицей корреляции, заданной как 𝐶𝑜𝑟(𝑥_𝑗1, 𝑥_𝑗2) = . Рассматриваются независимые и одинаково распределённые ошибки, сгенерированные из стандартного нормального распределения. Этот эксперимент повторяется 30 раз.

Таблица 1 резюмирует теоретические значения важности каналов, предложенные 𝛽², 𝜌², 𝛽 ∙ 𝜌, а также усреднённые значения анализа доминирования (DA) и относительного веса (RW) за 30 повторений. Отметим, что все значения важности были нормализованы так, чтобы в сумме давать единицу. Как упоминалось ранее, 𝛽², 𝜌² и 𝛽 ∙ 𝜌 не подходят в качестве эффективных мер, что можно подтвердить, изучив значения важности переменных 𝑥₃ и 𝑥₄. Как видно, является наименьшим квадратом коэффициента (незначительным), но квадрат корреляции 𝑥₃ с зависимой переменной является третьим по величине, что указывает на достаточно сильную связь с 𝑦. Использование только могло бы исказить истинную связь. В то время как для 𝑥₄ мы наблюдаем нулевую квадратную корреляцию, но достаточно большой , что показывает относительно большое влияние на прогнозирование 𝑦. Эти проблемы решаются в DA и RW. Они каким-то образом объединяют информацию, передаваемую как 𝛽, так и 𝜌, а также взаимодействия между переменными, что приводит к относительно небольшим, но не незначительным значениям важности для 𝑥₃ и 𝑥₄.

Таблица 1: Сравнение значений относительной важности для примера моделирования 1.

Каналы	𝛽	𝛽2	𝜌2	𝛽 ∙ 𝜌	DA	RW
x2	-4.5	0.372	0.432	0.474	0.342 (0.041)	0.344 (0.058)
x3	-0.5	0.005	0.108	0.026	0.054 (0.027)	0.069 (0.033)
x4	3.0	0.165	0.000	0.000	0.091 (0.021)	0.086 (0.027)
x5	-4.0	0.294	0.432	0.421	0.354 (0.056)	0.374 (0.081)

Кроме того, в таблице 1 приведены стандартные отклонения значимости по методам DA и RW на основе 30 повторений (указаны в скобках). Как обсуждается в литературе, у DA известны асимптотические свойства. То есть, по мере увеличения размера выборки набора данных, оценщики DA сходятся к теоретическим значениям DA. С другой стороны, у RW есть свойства сходимости валидности, и во многих случаях он обычно дает результаты, очень похожие на результаты DA.

Поэтому исследователи склонны делать вывод о том, что они измеряют одни и те же величины (Джонсон и Лебретон, 2004). Наши числовые результаты показывают, что эти два метода последовательно предлагают очень близкие значения относительной значимости, хотя оценщики RW, как правило, обладают более высокой изменчивостью, чем оценщики DA.

4.2 Пример моделирования 2: Методы относительной важности для сильно коррелированных данных

Мы рассматриваем симулированный пример с высокой корреляцией между переменными и показываем, что методы DA и RW учитывают это при расчете значений атрибуции, в то время как традиционные методы не способны это сделать. Чтобы создать более экстремальный симулированный набор данных, мы модифицируем матрицу корреляций в предыдущем примере так, что 𝐶𝑜𝑟(𝑥_𝑗1, 𝑥_𝑗2) = 0.8 (то есть все пары переменных имеют одинаково высокую корреляцию). Этот симуляционный пример также повторяется 30 раз.

Таблица 2 представляет теоретические значения 𝛽², 𝜌², 𝛽 ∙ 𝜌 и средние значения и стандартные отклонения значений относительной важности за 30 повторений. Можно видеть, что методы DA и RW предлагают последовательные значения важности с низкой изменчивостью. Из-за высокой корреляции между ними недостаточно доказательств для четкого определения, какая переменная значительно важнее другой, просто глядя на коэффициенты. Другими словами, DA и RW могут учитывать взаимосвязь моделей. Это не относится к 𝛽², и 𝜌². Наконец, отмечаем, что 𝜷 ∙ 𝝆 не является эффективной мерой, так как были получены отрицательные значения, что трудно интерпретировать на практике.

Таблица 2: Сравнение значений относительной важности для примера моделирования 2.

Каналы	𝛽	𝛽2	𝜌2	𝛽 ∙ 𝜌	DA	RW
x1	3.0	0.165	0.096	-0.298	0.110 (0.011)	0.115 (0.018)
x2	-4.5	0.372	0.322	0.820	0.341 (0.029)	0.334 (0.034)
x3	-0.5	0.005	0.185	0.069	0.090 (0.015)	0.140 (0.023)
x4	3.0	0.165	0.096	-0.298	0.111 (0.014)	0.111 (0.013)
x5	-4.0	0.294	0.302	0.707	0.299 (0.028)	0.300 (0.037)

4.3 Пример моделирования 3: Методы относительной важности: Линейные и аддитивные модели

Этот пример моделирования сравнивает эффективность линейных и аддитивных моделей. Мы используем симулированный набор данных, созданный на основе сложной нелинейной модели следующим образом,

с 𝑓₁(𝑥) = 𝑥(1 − 𝑥), 𝑓₂(𝑥) = 2log(max(𝑥, 1)), 𝑓₃(𝑥) = 1 − exp(−𝑥), 𝑓₄(𝑥) = 2𝑥^2/5 и 𝑓₅(𝑥) = 𝑥. Функции 𝑓₂(⋅) − 𝑓₅(⋅) обычно используются как насыщающие и не насыщающие трансформации в маркетинговой практике, в то время как 𝑓₁(⋅) представляет произвольную нелинейную функцию. 𝜀 является ошибочным членом, следующим стандартному нормальному распределению. Сначала мы генерируем 1000 обучающих данных, в которых переменные 𝑥_𝑗 генерируются из стандартного нормального распределения с корреляционной матрицей, заданной как 𝐶𝑜𝑟(𝑥_𝑗1, 𝑥_𝑗2) = (1/2)^{|𝑗1−𝑗2|}. Мы применяем DA и RW с линейными и аддитивными моделями к этому обучающему набору. Мы используем 5-кратную кросс-валидацию для выбора количества внутренних узлов TPS в аддитивной модели. Для оценки эффективности модели мы генерируем тестовый набор данных из той же модели. Он состоит из тысячи наблюдений. Тестовая ошибка измеряется с использованием среднеквадратичной ошибки (RMSE). Более конкретно,

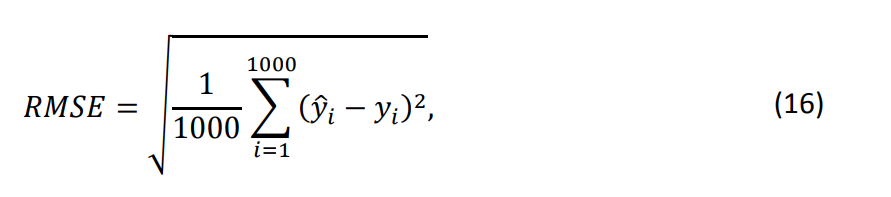
где 𝑦_𝑖, 𝑖 = 1, … ,1000 — истинные значения зависимой переменной в тестовом наборе данных, а 𝑦̂_𝑖, 𝑖 = 1, … 1000 — предсказанные значения. Мы повторяем эту тренировочно-тестовую симуляцию 30 раз.
где 𝑦_𝑖, 𝑖 = 1, … ,1000 — истинные значения зависимой переменной в тестовом наборе данных, а 𝑦̂_𝑖, 𝑖 = 1, … 1000 — предсказанные значения. Мы повторяем эту тренировочно-тестовую симуляцию 30 раз.

Таблица 3: Сравнение линейной и аддитивной моделей.

 

Каналы	ЛИНЕЙНАЯ МОДЕЛЬ		АДДИТИВНАЯ МОДЕЛЬ
	DA	RW	DA	RW
x1	0.191 (0.025)	0.199 (0.026)	0.289 (0.028)	0.279 (0.028)
x2	0.136 (0.013)	0.130 (0.013)	0.102 (0.010)	0.116 (0.009)
x3	0.402 (0.031)	0.400 (0.032)	0.396 (0.037)	0.384 (0.041)
x4	0.105 (0.014)	0.099 (0.014)	0.099  (0.016)	0.102  (0.011)
x5	0.166  (0.019)	0.173  (0.020)	0.114  (0.015)	0.118  (0.015)
R2	0.614  (0.045)		0.959  (0.039)
RMSE	0.646  (0.025)		0.959  (0.039)

 

Таблица 3 представляет относительную важность переменных (каналов), 𝑅² подогнанных моделей и RMSE. Аналогично, мы сообщаем средние значения и стандартные отклонения за 30 повторений. Как сообщается, линейные и аддитивные модели предлагают схожие, но несколько различные значения относительной важности. Мы наблюдаем, что аддитивная модель обеспечивает лучшее соответствие данным и более высокую предсказательную точность. Это связано с тем, что аддитивная модель, имея меньше параметрических ограничений, является более гибкой, позволяя данным выбирать подходящие функциональные компоненты. С более высокими значениями 𝑅² и предсказательной способностью, значения важности, предложенные аддитивной моделью, являются более достоверными. Это также наиболее вероятно будет верно при анализе любых реальных данных, которые обычно имеют более сложные внутренние взаимосвязи, чем наш пример симуляции.

 

4.4 Реальные данные: Групповой анализ

 

В этом разделе мы применяем все вышеупомянутые методы к реальному набору данных. Данные, которые мы используем, представляют собой записи на уровне событий онлайн-пользователей с идентификаторами отслеживания, генерирующими доход, из трехмесячной кампании, а также данные о воздействии на пользователей 18 рекламных каналов. Эти каналы группируются в три категории: издатели, DSP (системы управления спросом), платный поиск. Мы предварительно обрабатываем сырые данные, сопоставляя уникальные идентификаторы каналов и группируя их в соответствии с пользователями, чтобы можно было отслеживать доходы и воздействия для каждого пользователя. В результате у нас получилось всего 153 891 наблюдение, генерирующее доход. Таблица 4 представляет подробное описание набора данных. Обратите внимание, что общий доход для каждой категории в таблице не следует путать с атрибуционной стоимостью. Он содержит доход от всех пользователей, посетивших эту категорию. Однако эти пользователи могли посетить и другие категории, так что их доход может быть учтен более одного раза.

 

Таблица 4. Сводка данных

 

	Паблишеры	DSP	PAID SEARCH	ОБЩИЙ
Общий доход (М$)	2.2	6.2	6.8	14
Показ	1.0 ∗ 105	8.5 ∗ 105	9.7 ∗ 104	1.1 ∗ 106
Средний доход за показ ($)	21	7.2	69	14

 

Важной практической проблемой с реальными данными является то, что некоторые каналы могут иметь отрицательные коэффициенты в линейных моделях. Поскольку предложенные подходы основаны на разложении 𝑅2 с гарантированным отсутствием отрицательности, они всегда производят неотрицательные значения атрибуции. Однако отрицательные коэффициенты трудно интерпретировать и использовать на практике в планировании медиаинвестиций, особенно при расчете возврата инвестиций (ROI) для каждого отдельного канала. Поэтому мы дополнительно создаем гибридные значения атрибуции в дополнение к первоначальным результатам. Мы фильтруем каналы более точно, оставляя только те, у которых положительные регрессионные коэффициенты, а затем нормализуем их значения атрибуции, в то время как остальным каналам мы не присваиваем атрибуцию.

 

Мы используем предложенные методы: (i) DA с линейными моделями (DALM), (ii) DA с аддитивными моделями (DAAM), (iii) RW с линейными моделями (RWLM) и (iv) RW с аддитивными моделями (RWAM), для расчета значений атрибуции упомянутых групп рекламных каналов. Мы представляем полученные относительные значения атрибуции, время выполнения и коэффициент детерминации (R²) в таблице 5.

 

Таблица 5: Относительные значения атрибуции для группового анализа

 

ГРУППА КАНАЛОВ	𝛽	DA		RW
		ЛИНЕЙНЫЙ	АДДИТИВНЫЙ	ЛИНЕЙНЫЙ	АДДИТИВНЫЙ
Паблишеры	5.4%	0.62%	2.1%	0.64%	2.5%
DSP	38%	29%	33%	29%	35%
Paid Search	57%	71%	65%	71%	62%
Время выполнения	0.11s	0.35s	3.5mins	0.11s	2.7mins
R2	—	0.06	0.15	0.06	0.15

Значения атрибуции также представлены на рисунке 1. Как мы видим, все предложенные методы последовательно указывают, что платный поиск имеет наибольшую атрибуционную стоимость, которая составляет как минимум 62%, за ним следуют DSP (не менее 29%) и издатели (менее 3%).

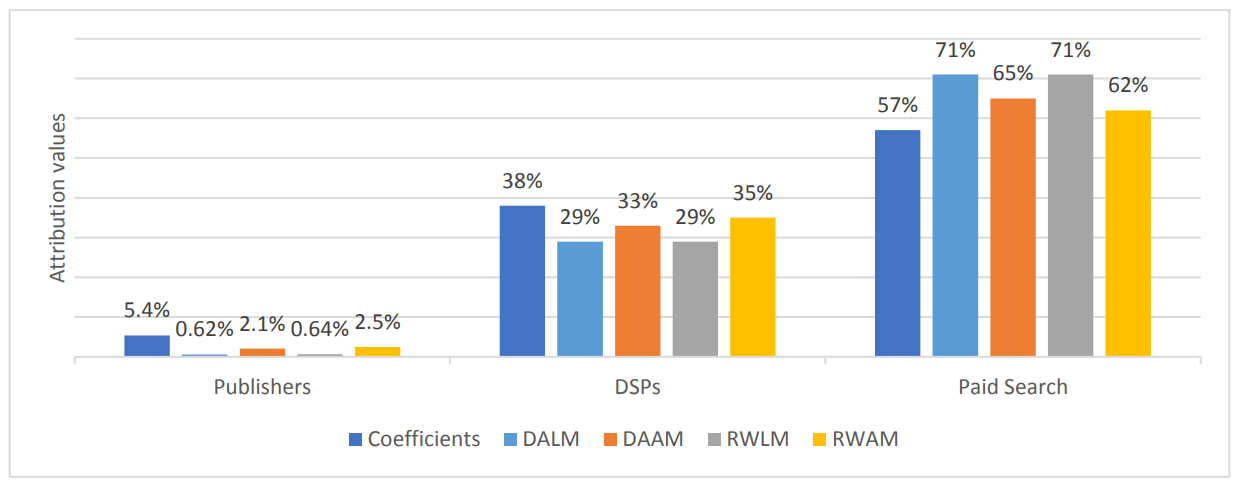
Сравнивая значения атрибуции, полученные из одних и тех же регрессионных моделей (т.е. DALM против RWLM и DAAM против RWAM), мы замечаем, что значения атрибуции, предложенные одной и той же структурой модели, очень близки.

Мы замечаем очевидные различия в значениях атрибуции, а также в соответствии моделей при сравнении результатов между различными моделями. В частности, аддитивные модели склонны уделять больше внимания DSP (около 34%) и издателям (около 2,3%), при этом снижая значение атрибуции для платного поиска до примерно 64%. Хотя обоснование результатов на основе реальных данных обычно сложно, метод аддитивной модели разложения атрибуций естественным образом описывает более точное соответствие истинной основной связи и, таким образом, может быть более достоверным.

Как мы уже упоминали ранее, DA испытывает большую вычислительную нагрузку, чем RW. Это может стать еще хуже с увеличением количества каналов. Следовательно, DA менее предпочтителен для применения в крупномасштабных приложениях.

4.5 Реальные данные: Анализ по всем каналам

Вместо того чтобы приписывать доход к группам каналов, мы проводим анализ всех каналов для того же набора данных, что и в предыдущем разделе. В частности, мы применяем RWLM и RWAM для анализа того, как доход должен быть распределен между 18 рекламными каналами. Поскольку DA всегда дает результаты, очень близкие к результатам RW, но при этом требует значительно больших вычислительных затрат (и эти затраты экспоненциально увеличиваются с ростом числа независимых переменных для оценки), мы решили не использовать DALM и DAAM в этом разделе. Каналы обозначены как P1, P2 и т.д. для тех, которые принадлежат издателям, D1 для канала от DSP, а S1 и S2 для каналов, относящихся к платному поиску.

На рисунке 2 мы показываем рассчитанные значения атрибуции для RWLM и RWAM, а соответствующие данные представлены в таблице 6. Обе модели последовательно отмечают S1, S2 и D1 как три канала с наивысшей атрибуцией. Тем не менее, мы также видим некоторые несоответствия в значениях атрибуции. В частности, RWLM присваивает значительно большее значение атрибуции каналу S1 по сравнению с RWAM (45% против 35%). В то время как значения атрибуции для D1 и S2 от RWLM и RWAM находятся близко друг к другу. Атрибуции этих трех каналов ближе друг к другу в модели RWAM, чем в RWLM.

Важное наблюдение заключается в том, что некоторые каналы (P10, P13, P14 и P15) имеют отрицательные регрессионные коэффициенты. Фактически, эти каналы все отрицательно коррелируют с зависимой переменной и, таким образом, потенциально могут вносить отрицательный вклад в доход. Это также может быть связано с тем, что P10, P13, P14 и P15 сильно коррелируют с другими каналами, так что их положительный маржинальный вклад может быть поглощен другими. Как и ожидалось, как показано в таблице 6, фактические значения атрибуции этих каналов незначительны. Как упоминалось ранее, мы решили дополнительно получить гибридные результаты, исключив эти четыре канала и нормализовав значения атрибуции для остальных.

Обратите внимание, что мы не включаем каналы со значениями атрибуции
менее 1% из-за нехватки места.

Таблица 6: Значения атрибуции для общеканального анализа

 

Канал	𝛽	RWLM		RWAM
		Raw	Hybrid	Raw	Hybrid
P1	0.21%	0.010%	0.010%	0.17%	0.17%
P2	5.9%	1.8%	1.9%	4.4%	4.5%
P3	0.35%	0.030%	0.030%	0.41%	0.42%
P4	2.3%	0.26%	0.26%	0.44%	0.45%
P5	0.49%	0.010%	0.010%	0.091%	0.091%
P6	2.1%	0.20%	0.20%	0.52%	0.53%
P7	2.1%	0.24%	0.24%	0.30%	0.30%
P8	3.7%	0.74%	0.75%	2.5%	2.6%
P9	2.3%	0.29%	0.29%	0.60%	0.61%
P10	0%	0.86%	0%	0.66%	0%
P11	2.3%	0.20%	0.20%	1.1%	1.1%
P12	1.7%	0.16%	0.16%	0.69%	0.70%
P13	0%	0.15%	0%	0.14%	0%
P14	0%	0.051%	0%	0.50%	0%
P15	0%	0.070%	0%	0.18%	0%
D1	24%	27%	27%	30%	31%
S1	30%	44%	45%	34%	35%
S2	23%	24%	24%	23%	23%

5 Заключение и дискуссия

В данной работе мы разработали несколько алгоритмических методов для распределения рекламных показов по множественным каналам с использованием моделей атрибуции. Предложенные подходы служат связующим звеном между моделированием атрибуции в маркетинге и соответствующими методологиями, разработанными в статистике. Более того, они обеспечивают более точный обзор нашей проблемы многокасательной атрибуции, улавливая совместные встречаемости и другие взаимодействия между рекламными каналами. Мы реализуем методы относительной важности, включая анализ доминирования и анализ относительного веса, с расширением до полупараметрических (аддитивных) моделей. Наша работа может быть потенциально расширена до гораздо более широкого пула регрессионных моделей, которые могут оказаться полезными для маркетинговых исследователей. В частности, анализ доминирования может быть легко применен к другим типам регрессионных моделей, таким как частично линейные аддитивные модели, модели с переменными коэффициентами и другие. В то время как анализ относительного веса обычно хорошо работает для линейных моделей: те, которые линейны по коэффициентам, такие как модели маркетингового микса, векторные авторегрессионные модели и другие.

Отмечаем, что предложенные подходы имеют некоторые врожденные преимущества и ограничения в плане масштабируемости. Временная производительность анализа доминирования быстро ухудшается с увеличением количества каналов. Однако метод легко масштабируется на огромное количество пользователей, если количество каналов остается постоянным. С другой стороны, анализ относительного веса легко масштабируется на множество каналов. Однако вычислительная нагрузка увеличивается с увеличением количества пользователей (объема). В принципе, анализ доминирования подходит для анализа с большим объемом и меньшим количеством каналов, в то время как анализ относительного веса практичен для анализа с меньшим объемом и большим количеством каналов.

Одной из общих сильных сторон двух предложенных данных, основанных на доходах моделей атрибуции, помимо точного учета взаимосвязей, выявленных через модели атрибуции, является их согласованность и устойчивость при повторных выборках. В нескольких случаях использования мы последовательно сообщали о сравнительно близких значениях атрибуции. Таким образом, предложенные подходы могут масштабироваться как для «больших данных», так и для «омниканального» анализа. Более точные и согласованные значения атрибуции также помогут рекламным практикам принимать более обоснованные решения в стратегии и планировании рекламы.

Источник: Ссылка