Открывая мир Цепей Маркова: понимание и применение в атрибуции

Атрибуция стала краеугольным камнем в мире маркетинга, она помогает нам определить вклад каждого канала в общий успех нашего бизнеса. Но как можно глубже проникнуть в эту многомерную проблему и выявить истинные взаимосвязи между различными маркетинговыми каналами? Ответ прячется в математических моделях, а именно — Цепях Маркова.

В этом гайде мы отправимся в увлекательное путешествие к сердцу маркетинговой аналитики, где Цепи Маркова станут нашим надежным компасом. Этот мощный инструмент позволяет нам преобразовать сложные пользовательские пути в понятные и интерпретируемые данные, что в конечном итоге помогает более точно определить влияние каждого канала на конечную конверсию.

Хотя Цепи Маркова могут показаться сложными, их основная идея довольно проста: будущее зависит только от текущего состояния, а прошлое остается за кадром. Вместе мы разберемся, как применить этот принцип на практике и как использовать Цепи Маркова для атрибуции в маркетинге. Этот гайд поможет вам глубже понять влияние ваших маркетинговых усилий на общую выручку и принимать более обоснованные решения о распределении бюджетов. Приготовьтесь к глубокому погружению в мир маркетинговой аналитики!

Введение в Цепи Маркова

Цепи Маркова – это математическая модель, которая описывает последовательность событий, где вероятность каждого последующего события зависит только от состояния, достигнутого в предыдущем событии. Впервые они были представлены русским математиком Андреем Андреевичем Марковым в начале XX века, и были названы в его честь.

Основной идеей цепей Маркова является принцип «без памяти», что означает, что будущее состояние системы зависит только от текущего состояния, и не затрагивает предыдущие состояния. Иными словами, «Будущее независимо от прошлого, если зафиксировано настоящее».

Цепи Маркова нашли широкое применение в различных областях, таких как статистика, экономика, информатика, физика и, конечно же, маркетинг. Они используются для прогнозирования погоды, анализа финансовых рынков, моделирования компьютерных сетей, а также для анализа последовательности веб-страниц, просмотренных пользователем, или пути пользователя от первого контакта с брендом до конверсии.
Одним из примеров использования цепей Маркова в маркетинге является модель атрибуции, которая позволяет определить вклад каждого канала в конечную конверсию. Это помогает маркетологам лучше понять, какие каналы наиболее эффективны, и принимать более обоснованные решения о распределении бюджета.

Полная вероятность совершения конверсии
Давайте разберемся с основами Цепей Маркова на примере из маркетинга (см. Рисунок 1). Возьмем три основных состояния: переход из рекламы на поиске (РП), переход из органического поиска (ОП) и прямой заход (ПЗ). Кроме того, добавим три специальных состояния:

• Start (начальное состояние),
• Conversion (целевое действие),
• Null (цепочка заканчивается без конверсии).

Вероятности переходов в этом примере следующие:
Из состояния «Start»:

• P(Start -> Реклама на поиске) = 1 (начинаем всегда с рекламы на поиске)

Из состояния «Реклама на поиске»:

• Вероятность перейти в Прямой заход: 0.8
• Вероятность перейти в Органический поиск: 0.2

Из состояния «Прямой заход»:

• Вероятность перейти в Null (цепочка заканчивается без конверсии): 0.9
• Вероятность перейти в Conversion (совершить целевое действие): 0.1

Из состояния «Органический поиск»:

• Вероятность перейти в Conversion (совершить целевое действие): 0.3
• Вероятность перейти в Null (цепочка заканчивается без конверсии): 0.7

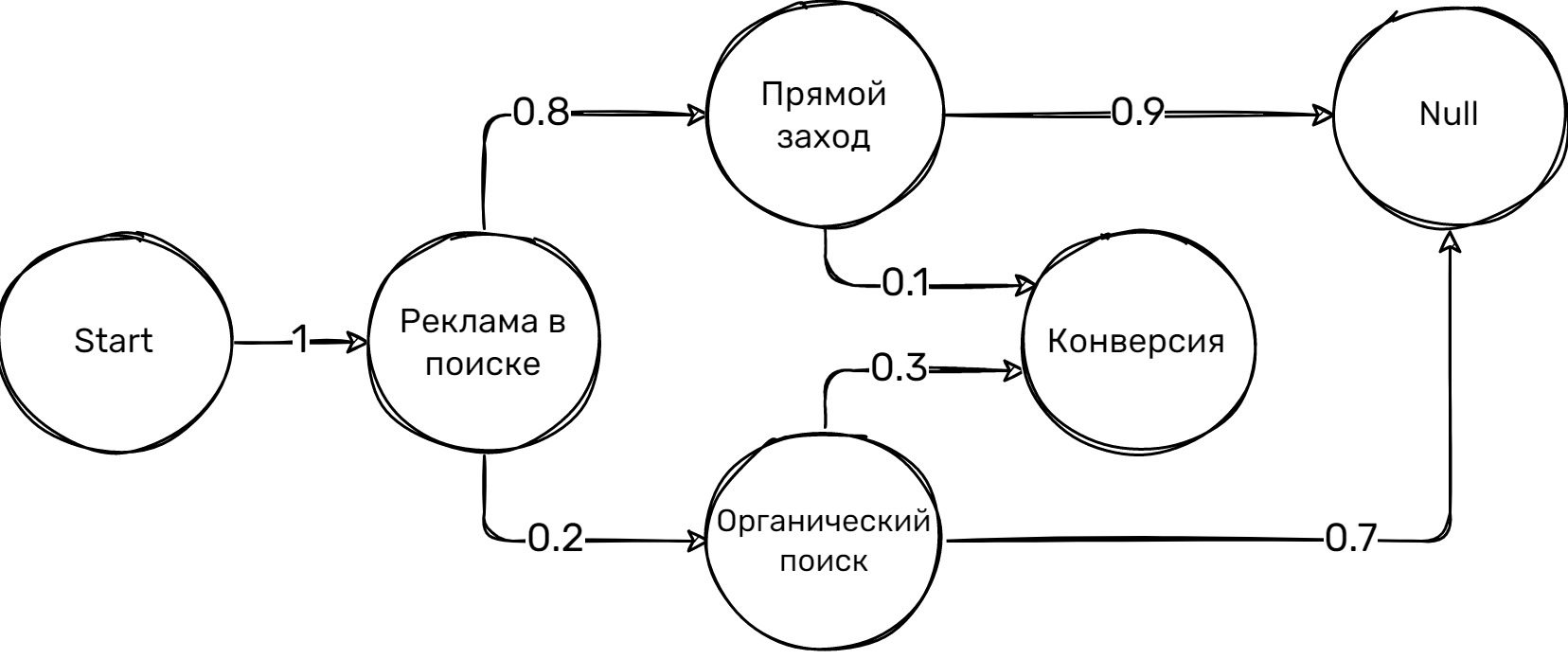
Для этого примера рассмотрим два пути: один, который заканчивается конверсией, и один, который заканчивается без конверсии:

• Путь с конверсией: Реклама на поиске (РП) -> Прямой заход (ПЗ) -> Conversion (C)
• Путь без конверсии: Реклама на поиске (РП) -> Органический поиск (ОП) -> Null (N)

Теперь объясним, что это за цепочка посещений:

• Путь с конверсией: клиент сначала перешел на сайт из рекламы на поиске, затем вернулся на сайт через прямой заход (например, ввод URL в браузер или клик по закладке), и в итоге совершил конверсию (например, покупку или регистрацию).
• Путь без конверсии: клиент сначала перешел на сайт из рекламы на поиске, затем вернулся на сайт через органический поиск (например, ввод запроса в поисковой системе), и в итоге ушел с сайта без совершения конверсии.

Рассчитаем вероятность каждого пути:

1. РП -> ПЗ -> C: P(РП -> ПЗ) * P(ПЗ -> C) = 0.8 * 0.1 = 0.08 (вероятность составляет 8%)
2. РП -> ОП -> N: P(РП -> ОП) * P(ОП -> N) = 0.2 * 0.7 = 0.14 (вероятность составляет 14%)

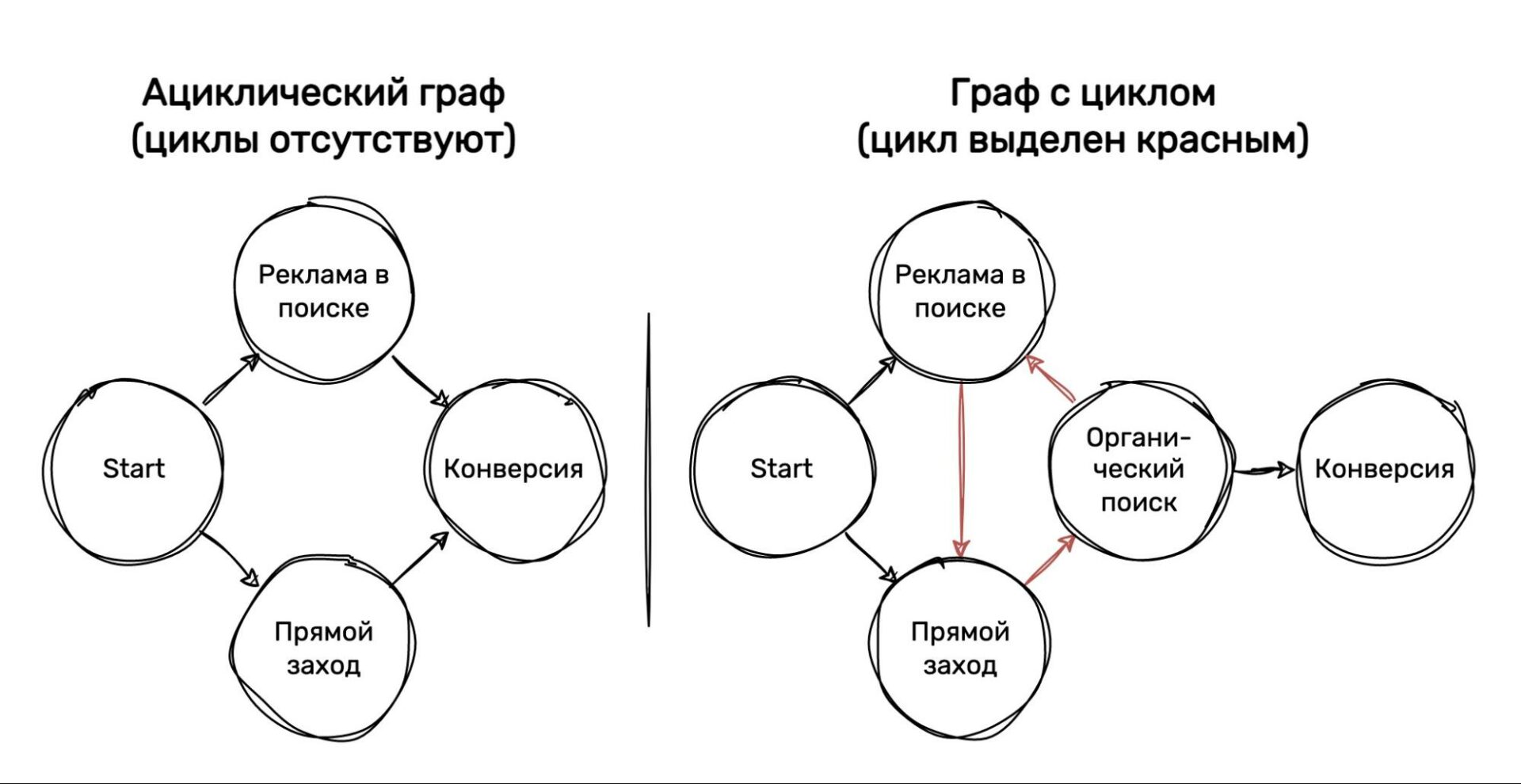
В контексте Цепи Маркова, полная вероятность — это вероятность достижения конкретного состояния (например, конверсии) через любой возможный путь. В этом случае, мы учитываем все возможные пути, по которым пользователь может пройти, чтобы достичь конечного состояния. Однако, стоит отметить, что полную вероятность можно рассчитать только для направленного ациклического графа, то есть графа без циклов (см. Рисунок 2).

При расчете полной вероятности важно учесть все возможные пути, которые могут привести к данному состоянию, и затем сложить вероятности каждого из этих путей. Это позволяет оценить вероятность события в более общем виде, учитывая различные варианты поведения пользователя и маркетинговые каналы, через которые пользователь мог взаимодействовать с сайтом.
Для нашего примера, чтобы рассчитать полную вероятность конверсии, нужно учесть все возможные пути, которые могут привести к состоянию «Conversion», и сложить вероятности этих путей. Мы уже рассмотрели один из возможных путей (РП -> ПЗ -> C) и рассчитали его вероятность (8%). Однако, могут быть и другие пути, ведущие к конверсии, и их вероятности также должны быть учтены при расчете полной вероятности.
В данном случае, существуют два возможных пути:

1. Реклама на поиске (РП) -> Прямой заход (ПЗ) -> Conversion (C)
2. Реклама на поиске (РП) -> Органический поиск (ОП) -> Conversion ©

Теперь рассчитаем вероятности для каждого пути:

1. РП -> ПЗ -> C: P(РП -> ПЗ) * P(ПЗ -> C) = 0.8 * 0.1 = 0.08
2. РП -> ОП -> C: P(РП -> ОП) * P(ОП -> C) = 0.2 * 0.3 = 0.06

Полная вероятность совершения конверсии равна сумме вероятностей каждого пути:
P(C) = 0.08 + 0.06 = 0.14
Таким образом, полная вероятность совершения конверсии составляет 14%.

Направленные графы с циклами и поглощающими состояниями

Перейдем к более сложному примеру, в котором мы рассмотрим поглощающие состояния и отличие направленных графов с циклами от ациклических графов (см. Рисунок 3).

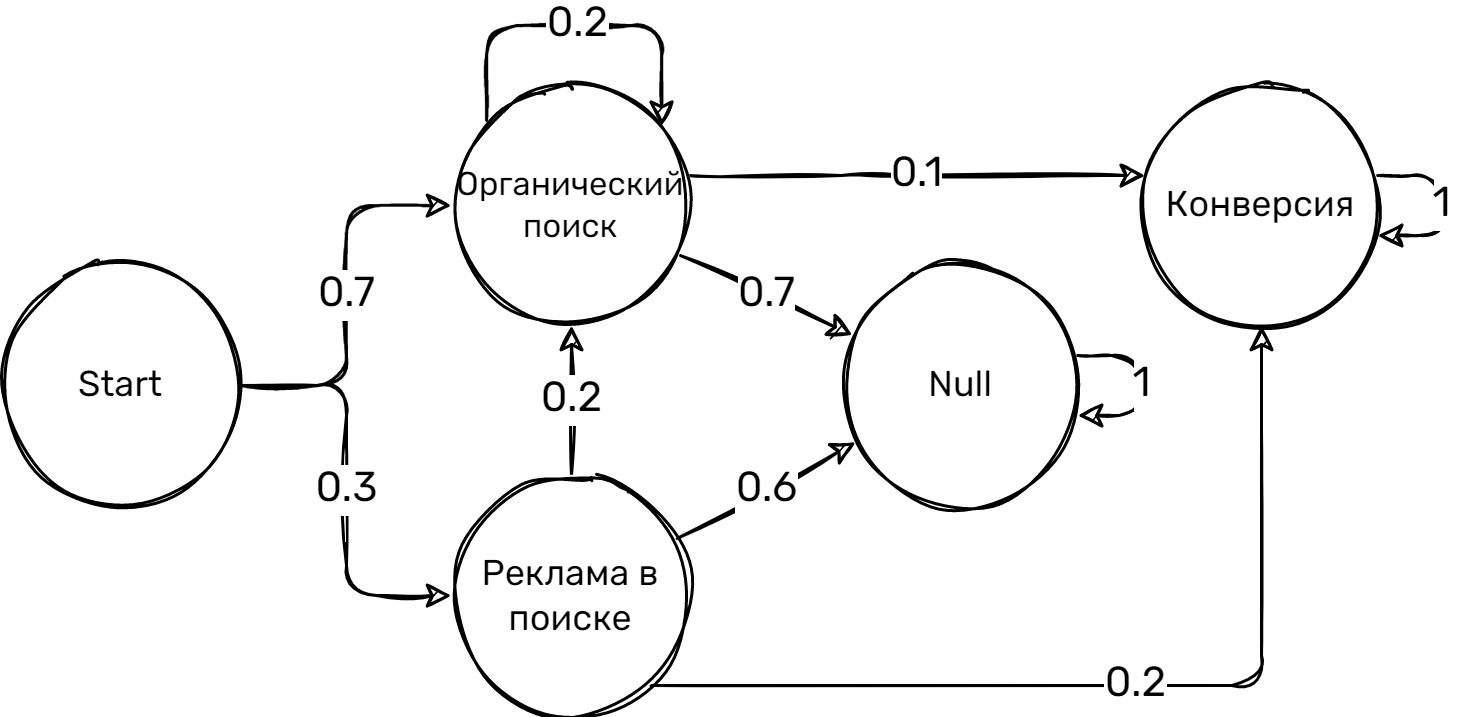
Вероятности переходов в этом примере следующие:
Из состояния «Start»:

• P(Start -> Органический поиск) = 0.7
• P(Start -> Реклама в поиске) = 0.3

Из состояния «Органический поиск» (порождает циклы):

• Вероятность остаться в Органическом поиске: 0.2
• Вероятность перейти в Конверсию: 0.1
• Вероятность перейти в Null: 0.7

Из состояния «Реклама в поиске»:

• Вероятность перейти в Органический поиск: 0.2
• Вероятность перейти в Null: 0.6
• Вероятность перейти в Конверсию: 0.2

Из состояния «Null» (поглощающее состояние):

• Вероятность остаться в Null: 1

Из состояния «Конверсия» (поглощающее состояние):

• Вероятность остаться в Конверсии: 1

Давайте начнем с объяснения поглощающих состояний и разницы между направленными графами с циклами и ациклическими направленными графами.

Поглощающие состояния – это такие состояния, из которых невозможно сделать переход в другие состояния. В нашем случае, «Конверсия» и «Null» являются поглощающими состояниями, потому что вероятность остаться в этих состояниях равна 1, и нет переходов в другие состояния.

Направленный граф с циклами – это ориентированный граф (орграф), в котором присутствуют циклы (контуры — циклически ориентированные маршруты), то есть возможность возврата в одно и то же состояние через один или несколько переходов. В ациклическом направленном графе циклы отсутствуют, и каждое состояние может быть посещено только однажды.

В предложенном примере мы имеем дело с направленным графом, в котором могут возникать циклы, потому что состояние «Органический поиск» может повторяться (вероятность перехода из «Органический поиск» в «Органический поиск» равна 0.2).

Для расчета полной вероятности конверсии, нужно учесть все возможные пути, которые могут привести к состоянию «Конверсия», и сложить вероятности этих путей. Однако, в данном случае, мы столкнемся с проблемой, связанной с наличием цикла в графе, что усложняет расчет, поскольку количество путей становится бесконечным. В реальных ситуациях, часто можно ограничить количество рассматриваемых путей, исходя из логики задачи или предполагаемой длительности пользовательской сессии.

Для определения полной вероятности конверсии, мы можем использовать методы, такие как матричное возведение в степень или итерационный алгоритм, чтобы найти стационарное распределение вероятностей. Это позволит нам определить вероятность того, что пользователь окажется в состоянии «Конверсия» после прохождения определенного количества переходов или через определенное время.

Стационарное состояние мы рассмотрим и рассчитаем далее, а пока мы можем рассчитать вероятность нахождения в том или ином состоянии через N шагов, начиная из состояния Start.

Давайте рассчитаем вероятность нахождения в состоянии «Конверсия» через 1, 2 и 3 шага.

1. Через 1 шаг:

P(Start -> Конверсия) = 0, так как нет прямого перехода из Start в Конверсия.

2. Через 2 шага:

• P(Start -> Органический поиск -> Конверсия) = P(Start -> Органический поиск) * P(Органический поиск -> Конверсия) = 0.7 * 0.1 = 0.07
• P(Start -> Реклама в поиске -> Конверсия) = P(Start -> Реклама в поиске) * P(Реклама в поиске -> Конверсия) = 0.3 * 0.2 = 0.06

Итак, вероятность нахождения в состоянии «Конверсия» через 2 шага равна 0.07 + 0.06 = 0.13

3. Через 3 шага:

Здесь возможны разные пути, и мы должны учесть все вероятности переходов. Возьмем только те пути, которые приводят к конверсии:

• Start -> Органический поиск -> Органический поиск -> Конверсия
• Start -> Реклама в поиске -> Органический поиск -> Конверсия
• Start -> Органический поиск -> Конверсия -> Конверсия
• Start -> Реклама в поиске -> Конверсия -> Конверсия

Рассчитаем вероятности для каждого пути и сложим их:

• P(Start -> Органический поиск -> Органический поиск -> Конверсия) = 0.7 * 0.2 * 0.1 = 0.014
• P(Start -> Реклама в поиске -> Органический поиск -> Конверсия) = 0.3 * 0.2 * 0.1 = 0.006
• P(Start -> Органический поиск -> Конверсия -> Конверсия) = 0.7 * 0.1 * 1 = 0.07
• P(Start -> Реклама в поиске -> Конверсия -> Конверсия) = 0.3 * 0.2 * 1 = 0.06

Итак, вероятность нахождения в состоянии «Конверсия» через 3 шага равна 0.014 + 0.006 + 0.07 + 0.06 = 0.15
Таким образом, мы можем рассчитать вероятность нахождения в определенном состоянии через N шагов, учитывая различные пути переходов и их вероятности.

Эффект удаления — Removal Effect

Removal effect — это метод анализа влияния каналов на конечную конверсию. Он показывает, насколько изменится вероятность конверсии, если мы уберем определенный канал.

Для расчета removal effect для каналов «Органический поиск» и «Реклама в поиске» в случае из двух шагов, сначала рассчитаем вероятность конверсии без учета каждого из этих каналов:

1. Убираем канал «Органический поиск», теперь у нас только один путь:
   Start -> Реклама в поиске -> Конверсия = P(Start -> Реклама в поиске -> Конверсия) = 0.3 * 0.2 = 0.06
2. Убираем канал «Реклама в поиске». В этом случае остается один путь: Start -> Органический поиск -> Конверсия = P(Start -> Органический поиск -> Конверсия) = 0.7 * 0.1 = 0.07

Теперь рассчитаем removal effect для каждого канала:

• RE(«Органический поиск») = (P_общая — P_безОрганического) / P_общая = (0.13 — 0.06) / 0.13 ≈ 0.538
• RE(«Реклама в поиске») = (P_общая — P_безРекламы) / P_общая = (0.13 — 0.07) / 0.13 ≈ 0.462

Removal effect показывает, что «Органический поиск» вносит примерно 53.8% вклада в конечную конверсию, в то время как «Реклама в поиске» вносит около 46.2% вклада.

Теперь, когда мы разобрали основы Цепей Маркова и узнали, как использовать их для анализа влияния различных каналов на конверсию, давайте перейдем к реальным данным. В следующем разделе мы познакомимся с датасетом, который содержит информацию о взаимодействии пользователей с различными каналами. Мы будем использовать этот датасет для того, чтобы применить на практике знания о Цепях Маркова и проанализировать влияние каналов на конверсию. Это позволит нам сделать более обоснованные выводы и рекомендации относительно оптимизации маркетинговых стратегий и рекламных кампаний.

Полный подход к анализу

В процессе изучения различных статей на тему атрибуции цепей Маркова в Интернете, мы заметили, что большинство из них допускает ряд упрощений в отношении Марковских цепей. На наш взгляд, эти упрощения могут искажать результаты атрибуции. Давайте проанализируем типичные упрощения на примере.

Представим, что у нас есть исходный граф посещений пользователем веб-сайта (см. Рисунок 4). Вы заметите, что маркетинговые каналы, по которым пользователь приходит на сайт, могут чередоваться и повторяться. Это приводит к множеству разных переходов, например, от «Реклама в поиске» к «Реклама в видео», или от «Органический поиск» к «Органический поиск». Является ли редкостью ситуация, когда пользователь в рамках своей конверсионной цепочки сессий приходит из разных маркетинговых каналов? Ответ — нет. Нашей задачей является точное отслеживание всего пути, который проходит пользователь до конверсии, включая все комбинации источников и количество переходов между ними.

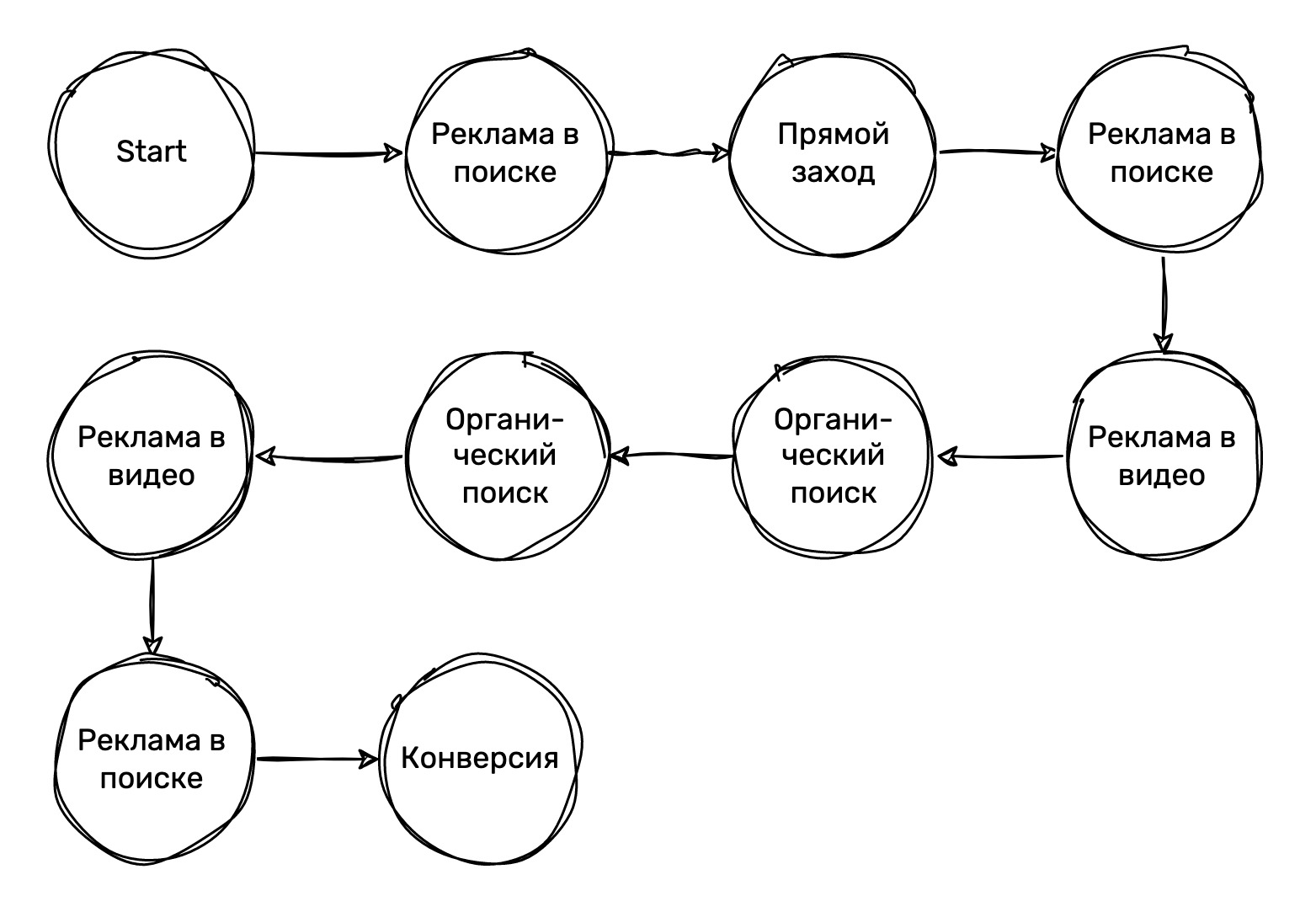
Можно задать себе вопрос: важно ли количество переходов? Ведь если пользователь пришел с рекламного поиска один раз или двадцать раз, но все равно совершил целевое действие, разница есть? Несомненно, она есть. Во-первых, мы имеем дело с разными рекламными бюджетами. Во-вторых, вероятность конверсии при посещении веб-сайта или приложения с определенного рекламного канала будет меняться. Если пользователь всегда совершает покупку сразу при первом посещении сайта с рекламы в поиске, это говорит о высоком конверсионном потенциале такого канала. Но если конверсия достигается только на двадцатом посещении, то процент сессий с таким источником, которые закончились конверсией, логически уменьшается в 20 раз.

Теперь давайте рассмотрим, как этот путь пользователя будет выглядеть после преобразований, которые предлагаются в других источниках. Как правило, в таких подходах обычно игнорируются повторные посещения из одного и того же канала, предпочитая упрощенные модели, в которых каждый канал посещается только один раз. Это приводит к потере ценной информации о взаимодействии пользователя с маркетинговыми каналами.

Если мы применим этот подход к нашему графу посещений, то потеряем детали о том, как именно пользователь «прыгал» между каналами, и сколько раз он делал это. Вместо полного и точного отображения пути пользователя мы получим упрощенную картину, которая может дать нам искаженное представление об эффективности различных маркетинговых каналов (см. Рисунок 5).

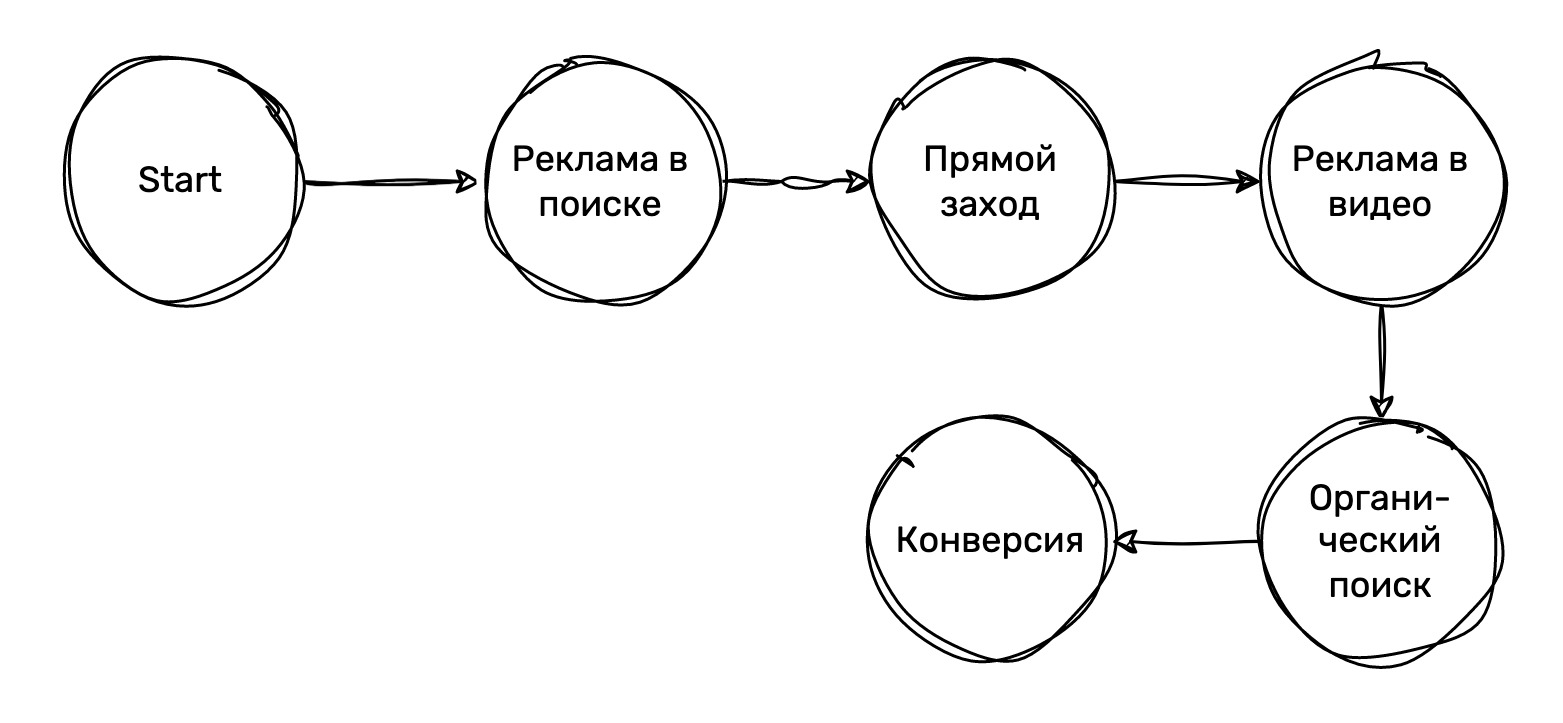
Преобразования, предлагаемые другими авторами для упрощения, обычно включают следующие шаги:

1. Путь пользователя представляется в виде одномерного массива или вектора. В нашем случае, такой вектор будет выглядеть следующим образом: [«Start», «Реклама в поиске», «Прямой заход», «Реклама в поиске», «Реклама в видео», «Органический поиск», «Органический поиск», «Реклама в видео», «Реклама в поиске», «Конверсия»]
2. Затем из этого вектора удаляются все повторяющиеся каналы, оставляя только те, которые встречаются впервые. В результате мы получаем: [«Start», «Реклама в поиске», «Прямой заход», «Реклама в видео», «Органический поиск», «Конверсия»]

Такой подход позволяет избавиться от циклов и упростить модель, но вместе с этим мы теряем значимую информацию о динамике взаимодействия пользователя с различными каналами.

В частности, мы теряем информацию о комбинациях переходов и частотности взаимодействия с каналами. В исходном графе, например, конверсию обеспечивает канал «Реклама в поиске», тогда как в упрощенной модели к конверсии приводит «Органический поиск». Мы также теряем информацию о переходах от «Органического поиска» к «Рекламе в видео» и от «Рекламы в видео» к «Рекламе в поиске».

Однако, наш подход к построению атрибуции на основе цепей Маркова сохраняет все эти детали. Мы учитываем все переходы между каналами, включая повторные, и учитываем их количество. Это позволяет нам создать более точную картину взаимодействия пользователя с маркетинговыми каналами и более корректно оценить их вклад в конверсию.

Все это делает нашу модель атрибуции на основе цепей Маркова более сложной, но и более точной, чем модели, которые вы можете встретить в других источниках. Мы уверены, что эта дополнительная точность стоит дополнительных усилий при построении модели.

Знакомство с датасетом

Вот пример данных из датасета, который мы будем использовать для анализа влияния различных каналов на конверсию с помощью Цепей Маркова:

Каждая строка данных представляет собой одно взаимодействие пользователя (clientId) с определенным каналом (source_text, medium_text) в определенное время (time). Также присутствует информация о рекламной кампании (campaign_text), ключевом слове (keyword), количестве совершенных транзакций (transactions) и выручке от этих транзакций (cur_revenue).

Нашей задачей будет преобразовать эти данные таким образом, чтобы мы могли применить модель Цепей Маркова для анализа влияния различных каналов на конверсию пользователей.

Глубина детализации атрибуции зависит от выбранных полей для анализа, таких как campaign_text, medium_text и source_text. В зависимости от вашей задачи и доступных данных, вы можете выбрать разные уровни детализации для атрибуции.

Например, если вы хотите анализировать только источник-канал (source_text, medium_text), вы сможете определить общую эффективность каждого канала в контексте атрибуции. Однако, если ваша цель – более детально разобраться в эффективности отдельных рекламных кампаний, то имеет смысл добавить поле campaign_text в анализ.

Если же вы хотите углубиться еще больше, можно рассмотреть атрибуцию на уровне ключевых слов (keyword). Это позволит оценить, какие именно запросы или группы запросов приводят к наиболее высокой конверсии и могут быть наиболее важными для вашего бизнеса.
Выбор уровня детализации атрибуции зависит от ваших бизнес-целей и доступных данных. Более глубокий анализ может помочь вам лучше понять, какие элементы вашей маркетинговой стратегии наиболее эффективны, и определить возможности для оптимизации и улучшения результатов.

Предобработка данных

Остановимся на уровне детализации, представленном в датасете, и перейдем к очень важному шагу – предобработке данных.

Предобработка данных является критически важным этапом в любом проекте анализа данных, так как она включает подготовку и очистку данных для последующего анализа и моделирования. На этом этапе мы обрабатываем пропущенные значения, обрабатываем выбросы, а также преобразуем и агрегируем данные для упрощения анализа.
В нашем случае, датасет уже содержит информацию о источниках, каналах и кампаниях, с которой мы можем работать. Однако, нам следует выполнить следующие шаги предобработки данных:

• Приведение значений столбцов ‘source_text’, ‘medium_text’, ‘campaign_text’ и ‘keyword’ к нижнему регистру для обеспечения единообразия данных.
• Удаление ‘www.’ из значений столбца ‘source_text’ для упрощения анализа источников трафика.
• Обработка значений, связанных с электронной почтой (email), в столбцах ‘source_text’ и ‘medium_text’. Если значения содержат ’email’ или ’eml’, они объединяются в ’email’.
• Применение словаря medium_preprocess_dict для стандартизации значений столбца ‘medium_text’.
• Фильтрация редких значений в столбцах ‘medium_text’ и ‘source_text’, используя пороговое значение 0.99.
• Создание столбца ‘ban_source’, который содержит информацию о том, принадлежит ли источник трафика к списку запрещенных источников или является прямым трафиком.
• Обработка столбца ‘cur_revenue’ для замены отрицательных значений на ноль.
• Сортировка данных по ‘clientId’ и ‘time’ для обеспечения правильного порядка сессий пользователей.

Banned_sources — это список источников трафика, которые были неправильно определены или случайно попали в UTM-метки из-за ошибок, таких как переадресация с сайта банка или других сторонних ресурсов. В действительности, такие источники трафика не должны учитываться при анализе атрибуции, так как они могут исказить результаты и привести к неверным выводам относительно эффективности маркетинговых каналов.

При предобработке данных мы создаем столбец ‘ban_source’, который отмечает, принадлежит ли источник трафика к списку запрещенных источников или является прямым трафиком. Это позволяет в дальнейшем исключить эти источники из анализа и улучшить точность модели атрибуции.

# Создаем словарь для предобработки medium_text
medium_preprocess_dict = {
   'cpc' : 'cpc',
   'cpm' : 'cpm',
   'social' : 'social',
   'cpa': 'cpa'
}

# Приводим все текстовые значения в нижний регистр
for col in ['source_text', 'medium_text', 'campaign_text', 'keyword']:
   data[col] = data[col].str.lower()

# Убираем "www." из source_text
data.loc[:, 'source_text'] = data['source_text'].str.replace('www.', '')

# Обрабатываем случаи с электронной почтой (email)
data['is_email'] = data['medium_text'].str.contains('email|eml')
data['is_email'] = (data['is_email'] + data['source_text'].str.contains('email|eml')).astype(bool)
data.loc[data['is_email'], 'campaign_text'] = data.loc[data['is_email'], 'source_text'] + '/' + data.loc[data['is_email'], 'campaign_text'].str.replace('(not set)', '')
data.loc[data['is_email'], 'source_text'] = 'email'
data.loc[data['is_email'], 'medium_text'] = 'email'
data.drop(columns=['is_email'], inplace=True)

# Применяем словарь для предобработки medium_text
for key in medium_preprocess_dict.keys():
   data.loc[data['medium_text'].str.contains(key), 'medium_text'] = medium_preprocess_dict[key]

# Фильтруем редкие значения в medium_text и source_text
data = filter_rare_values(data, cols=['medium_text', 'source_text'], threshold=0.99, combo=True)

# Обрабатываем banned_sources (запрещенные источники)
data['ban_source'] = 0
data.loc[((data['source_text'].isin(banned_sources['sources'])) | (data['source_text'] == '(direct)')), 'ban_source'] = 1

# Выбираем необходимые столбцы и обрабатываем отрицательные значения в cur_revenue
data = data[['clientId', 'time', 'source_text', 'medium_text', 'campaign_text', 'keyword', 'transactions', 'ban_source', 'cur_revenue']]
data['cur_revenue'] = data['cur_revenue'].apply(lambda x: max(x, 0))

# Сортируем данные по clientId и времени
data = data.sort_values(['clientId', 'time']).reset_index(drop=True)

Функция filter_rare_values предназначена для фильтрации редко встречающихся значений в данных на основе указанного порога. Она может быть применена к объектам типа pd.DataFrame или pd.Series. Важно отметить, что если входные данные представлены в виде DataFrame, необходимо указать столбцы, по которым будет проводиться фильтрация.

Основные параметры функции:

• data: Входные данные, которые могут быть DataFrame или Series.
• cols: Список столбцов, по которым нужно проводить фильтрацию. Если указан один столбец, он будет преобразован в список. Если используется DataFrame, этот параметр обязателен.
• threshold: Порог для фильтрации. Значения с частотой ниже этого порога будут удалены. Значение должно быть от 0 до 1 (по умолчанию 0.9).
• combo: Флаг для указания, должны ли столбцы фильтроваться вместе (True) или по отдельности (False, по умолчанию).

Функция работает следующим образом:

1. Если входные данные представлены в виде Series, они преобразуются в DataFrame с одним временным столбцом.
2. Функция проверяет, указаны ли столбцы для фильтрации, и вызывает ошибку, если не указаны.
3. Затем функция проверяет порог на корректность (от 0 до 1).
4. Если параметр combo равен False, функция фильтрует каждый столбец по отдельности. В противном случае она создает новый временный столбец, объединяющий значения всех указанных столбцов, и проводит фильтрацию по нему.
5. После удаления редких значений возвращается отфильтрованный DataFrame или Series.

Таким образом, функция filter_rare_values позволяет удалять редко встречающиеся значения в данных, что может быть полезно при анализе и предобработке данных перед моделированием.

def filter_rare_values(data: Union[pd.DataFrame, pd.Series],
                       cols: Optional[Union[str, List[str]]] = None,
                       threshold: float = 0.9,
                       combo: bool = False) -> Union[pd.DataFrame, pd.Series]:
    """
    Фильтрует редко встречающиеся значения в данных на основе указанного порога.

    Parameters
    ----------
    data : pd.DataFrame, pd.Series
        Входные данные, которые могут быть DataFrame или Series.
    cols : Optional[Union[str, List[str]]], default None
        Список столбцов, по которым нужно проводить фильтрацию. По умолчанию None.
    threshold : float, optional
        Порог для фильтрации. Значения с частотой ниже этого порога будут удалены.
        Значение должно быть от 0 до 1. По умолчанию 0.9.

    Returns
    -------
    Union[pd.DataFrame, pd.Series]
        Данные с отфильтрованными редко встречающимися значениями.
    """

    if isinstance(data, pd.Series):
        data = data.to_frame('temp_col')
        cols = ['temp_col']
     # Если указан один столбец, преобразуем его в список
    elif isinstance(cols, str):
        cols = [cols]

    # Если указан DataFrame, но не указаны столбцы для фильтрации, вызываем ошибку
    assert not (isinstance(data, pd.DataFrame) and cols is None), "When data is a DataFrame, cols must be specified."

    if not 0 <= threshold <= 1:
        raise ValueError("threshold must be between 0 and 1")

    index_to_remove = set()

    if not combo: 
        for col in cols:
            value_counts = data[col].value_counts(normalize=True).cumsum()
            valid_values = value_counts[value_counts > threshold].index
            col_valid_indices = data[data[col].isin(valid_values)].index
            index_to_remove.update(col_valid_indices)
    else:
        common_col = '__temp_filter_rare__'
        data[common_col] = data[cols[0]]
        for col in cols[1:]:
            data[common_col] += '//' + data[col]
        value_counts = data[common_col].value_counts(normalize=True).cumsum()
        valid_values = value_counts[value_counts > threshold].index
        col_valid_indices = data[data[common_col].isin(valid_values)].index
        index_to_remove.update(col_valid_indices)
        data.drop(columns=[common_col], inplace=True)
        
    filtered_data = data.drop(index_to_remove, axis=0)

    if len(cols) == 1 and 'temp_col' in cols:
        filtered_data = filtered_data.squeeze()

    return filtered_data

Функция filter_rare_values является универсальным и мощным инструментом, который может значительно облегчить вашу работу при анализе данных в различных бизнес-сценариях. Использование этой функции поможет вам справиться с неприятными выбросами и редко встречающимися значениями, что, в свою очередь, улучшит качество ваших аналитических моделей и принимаемых на их основе решений. Не упустите возможность применить эту функцию в своей работе, она станет незаменимым помощником при решении широкого круга задач анализа данных.

<h2>Создание цепочек сессий</h2>

Наш тестовый датасет для оценки вклада в конверсии мы лаконично назовем test.

При создании цепочек сессий, мы следуем нескольким простым шагам:
1. Сначала мы группируем сессии по клиентам и считаем количество транзакций для каждой группы:

test['transaction_group'] = test.groupby('clientId')['transactions'].cumsum()

2. Затем мы присваиваем каждой сессии номер, чтобы мы могли отслеживать их порядок внутри каждой группы:

test['order'] = test.groupby(['clientId', 'transaction_group'])['time'].cumcount() + 1

3. Далее мы определяем, является ли сессия началом группы или нет. Если это первая сессия в группе, то она является начальным узлом:

test['is_start_node'] = test['order'].apply(lambda x: True if x == 1 else False)

4. Если у сессии есть запрещенный источник и она не первая в группе, мы обнуляем информацию об источнике, канале, кампании и ключевом слове:

test.loc[(test['ban_source'] == 1) & (test['order'] != 1), ['source_text', 'medium_text', 'campaign_text', 'keyword']] = None

5. После этого мы заполняем пропущенные значения для этих полей, используя предыдущие значения в рамках группы клиентов:

test = ffill_se(test, ['source_text', 'medium_text', 'campaign_text', 'keyword'], 'clientId')

6. Затем мы создаем узел, объединяя информацию об источнике и канале:

test['node'] = test['source_text'] + '/' + test['medium_text']

7. Наконец, мы вычисляем следующий узел для каждой сессии в группе, сдвигая значения на одну позицию назад:

test['next_node'] = test.groupby(['clientId', 'transaction_group'])['node'].shift(-1)

8. Если следующий узел отсутствует, мы определяем, является ли сессия конверсией или выходом на основе количества транзакций:

test.loc[pd.isna(test['next_node']), 'next_node'] = test.loc[pd.isna(test['next_node'])].apply(lambda x: 'conversion' if x['transactions'] > 0 else 'out', axis=1)

Таким образом, мы получаем цепочки сессий, состоящие из узлов, которые связаны друг с другом в зависимости от порядка их появления.

Функция ffill_se (forward fill with separate edges) предназначена для заполнения пропущенных значений в определенных столбцах датафрейма, используя значения из предыдущих строк в рамках группы. Она аналогична методу fillna(method=’ffill’), но с одним важным отличием: она не переносит значения через границы групп, определенные по заданным столбцам.

def ffill_se(df, fill_cols, group_cols):
    """
    Заполняет пропущенные значения в указанных столбцах датафрейма, используя значения из предыдущих строк
    в рамках группы, определенной по заданным столбцам.
    
    Parameters
    ----------
    df : pd.DataFrame
        Исходный датафрейм, в котором нужно заполнить пропущенные значения.
    fill_cols : List[str]
        Список столбцов, в которых нужно заполнить пропущенные значения.
    group_cols : Union[str, List[str]]
        Столбец или список столбцов, по которым нужно сгруппировать данные для выполнения операции заполнения.
        
    Returns
    -------
    pd.DataFrame
        Датафрейм с заполненными пропущенными значениями.
    """

    # Вычисляет столбец с кумулятивной суммой непропущенных значений в рамках каждой группы
    nofill = pd.notnull(df[fill_cols[0]]).groupby(df[group_cols]).cumsum()

    # Заполняет пропущенные значения в указанных столбцах, используя метод ffill
    df[fill_cols] = df[fill_cols].fillna(method='ffill')

    # Сбрасывает значения на пропущенные, где группы начинаются с пропущенных значений
    df.loc[nofill==0, fill_cols] = np.nan

    return df

Давайте рассмотрим аргументы функции:

• df: исходный датафрейм, в котором нужно заполнить пропущенные значения.
• fill_cols: список столбцов, в которых нужно заполнить пропущенные значения.
• group_cols: столбец или список столбцов, по которым нужно сгруппировать данные для выполнения операции заполнения.

Алгоритм работы функции состоит из следующих шагов:

1. Вычисляет столбец с кумулятивной суммой непропущенных значений в рамках каждой группы. Это помогает определить, какие строки являются первыми в каждой группе.
2. Заполняет пропущенные значения в указанных столбцах, используя метод ffill. В этом случае значения могут быть перенесены через границы групп.
3. Сбрасывает значения на пропущенные, где группы начинаются с пропущенных значений, чтобы сохранить разделение между группами.

Функция ffill_se полезна, когда вам нужно заполнить пропущенные значения в датафрейме, но при этом сохранить разделение между группами данных.

Расчет вектора начального распределения трафика

Этот код вычисляет вектор начального распределения трафика, который показывает, как часто каждый узел является начальным узлом в цепочке сессий.

start_node_dist = test.groupby('node')['is_start_node'].sum() / test['is_start_node'].sum() 
start_node_dist = start_node_dist.rename('start').to_frame().transpose()

Другими словами, это распределение вероятностей того, с какого узла (источника и канала) пользователи начинают свой путь на сайте.
Для этого код выполняет следующие шаги:

1. Группирует данные по узлам (источнику и каналу) и суммирует значения в столбце is_start_node. Это позволяет определить, сколько раз каждый узел являлся начальным узлом в цепочке сессий.
2. Делит количество начальных узлов для каждого узла на общее количество начальных узлов, чтобы получить вероятности начала сессии с каждого узла.
3. Преобразует полученные данные в датафрейм и транспонирует его, создавая вектор начального распределения трафика.

Теперь у нас есть вектор начального распределения трафика, который может быть использован для дальнейшего анализа путей пользователей на сайте или для моделирования переходов между узлами.

Матрица переходов

Матрица переходов — это матрица, которая описывает вероятности перехода между различными состояниями или узлами в системе. В контексте анализа путей пользователей на сайте, узлы представляют собой комбинации источников трафика и каналов маркетинга, а матрица переходов показывает, насколько вероятно, что пользователь перейдет от одного узла к другому в процессе своей сессии.

Каждый элемент матрицы переходов находится на пересечении строки i и столбца j и представляет вероятность перехода от узла i к узлу j. Сумма всех элементов в строке равна 1, так как общая вероятность перехода от одного узла к любому другому узлу должна быть равна 100%.

Матрица переходов является основой для анализа путей пользователей и моделирования их поведения на сайте. С ее помощью можно оценить, насколько эффективны различные источники трафика и каналы маркетинга, а также определить возможные улучшения в стратегии продвижения сайта. В дополнение к этому, матрица переходов может быть использована для создания моделей марковских цепей, которые могут предсказать будущее поведение пользователей на сайте и помочь оптимизировать маркетинговые кампании.

В классической теории, для построения матрицы переходов, сначала нужно определить состояния или узлы, между которыми могут происходить переходы. Затем на основе имеющихся данных или наблюдений подсчитываются частоты переходов между этими состояниями. На основе этих частот рассчитываются вероятности переходов, которые затем заполняют матрицу переходов.

На практике, в коде, построение матрицы переходов осуществляется следующим образом:

1. Группировка данных по узлам и подсчет количества переходов между ними:

tr_matrix = test.groupby('node')['next_node'].value_counts().sort_values(ascending=False).unstack().fillna(0).sort_values('conversion', ascending=False)

2. Расчет вероятностей переходов в строках матрицы:

tr_matrix['all_transitions'] = tr_matrix.sum(axis=1)
for col in tr_matrix.columns:
    tr_matrix[col] /= tr_matrix['all_transitions']

3. Обработка случаев, когда нет данных о переходе от одного узла к другому:

for idx in tr_matrix.index:
    if idx not in tr_matrix.columns:
        tr_matrix[idx] = 0

4. Добавление специальных состояний (conversion, out) в матрицу:

special_states = ['conversion', 'out']
cols = tr_matrix.index.tolist() + special_states
tr_matrix = tr_matrix[cols]
for i, state in enumerate(special_states):
    if state not in tr_matrix.index:
        conv_idx = pd.Series(name=state, index=tr_matrix.columns, data=[0 for _ in range(len(tr_matrix.columns) - (len(special_states) - i))] + [1] + [0 for _ in range(len(special_states) - i - 1)])
        tr_matrix = tr_matrix.append(conv_idx)

5. Добавление начального состояния (start) в матрицу:

tr_matrix = pd.concat([tr_matrix, start_node_dist]).fillna(0)
tr_matrix['start'] = 0

После выполнения данных шагов мы получаем матрицу переходов, которая содержит вероятности перехода между различными состояниями (см. Рисунок 7).

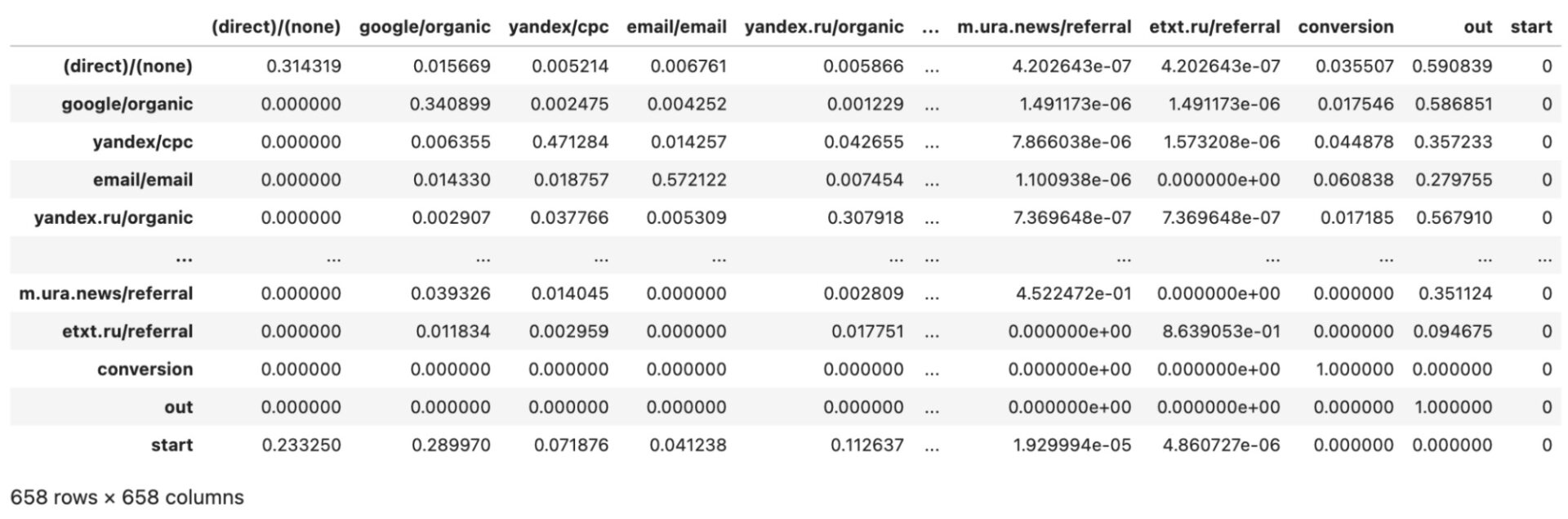
Эта матрица может быть использована для анализа путей пользователей на сайте и прогнозирования их дальнейшего поведения.

Рассчитываем вклад каналов в конверсию

После того как мы расчитали матрицу переходов, следующим важным понятием является стационарное состояние. Стационарное состояние — это такое состояние системы, в котором вероятности нахождения в каждом состоянии не меняются со временем, даже при многократных переходах между состояниями. В контексте анализа пользовательских путей стационарное состояние может помочь нам оценить, какие состояния являются наиболее «устойчивыми» или наиболее вероятными в долгосрочной перспективе.

Один из способов расчета стационарного состояния — многократное умножение матрицы переходов самой на себя. Суть этого подхода заключается в том, что при достаточно большом количестве умножений матрица переходов сходится к состоянию, в котором вероятности перехода между состояниями стабилизируются и перестают изменяться. Это позволяет нам определить стационарное состояние системы и оценить вероятности нахождения в различных состояниях в долгосрочной перспективе.

Связь removal effect и стационарного состояния заключается в том, что removal effect оценивает вклад каждого канала в конверсию, основываясь на изменении стационарного состояния при удалении этого канала из системы. Таким образом, стационарное состояние служит основой для оценки вклада различных каналов в конверсию.

Стационарное состояние может быть использовано для расчета вклада того или иного канала в конверсии, потому что оно представляет собой стабильное распределение вероятностей между состояниями системы. В нашем случае, состояние «конверсия» является одним из интересующих нас состояний. Если мы удалим один из каналов и пересчитаем стационарное состояние, мы сможем увидеть, как изменится вероятность конверсии без данного канала. Это изменение и будет являться вкладом канала в конверсию.

На практике, сначала мы вычисляем базовую конверсию с использованием стационарного состояния:

base_cr = np.linalg.matrix_power(tr_matrix.values, 50)[-1][-3]

Здесь мы возведем матрицу переходов в 50-ую степень и возьмем значение из строки «Start» и столбца «Conversion».

Далее, для каждого канала, мы удаляем его из матрицы переходов и снова вычисляем стационарное состояние без этого канала:

removal_matrix_cr = np.linalg.matrix_power(tr_matrix.drop(col, axis=1).drop(col, axis=0).values, 50)[-1][-3]

Затем мы считаем removal effect для каждого канала, сравнивая изменение конверсии с базовой конверсией:

res_dict[col] = 1 - removal_matrix_cr / base_cr

Таким образом, мы получаем словарь res_dict, где для каждого канала указан его вклад в конверсию в виде removal effect.

После того, как мы получили ранжирование каналов на основе их вклада в конверсию, мы можем визуализировать эти результаты с помощью горизонтального столбчатого графика. В данном случае, мы рассматриваем топ-10 каналов с самым высоким рейтингом по методу Маркова (см. Рисунок 8). Для удобства восприятие, значения были нормированы таким образом, чтобы максимальное значение равнялось 10 000.

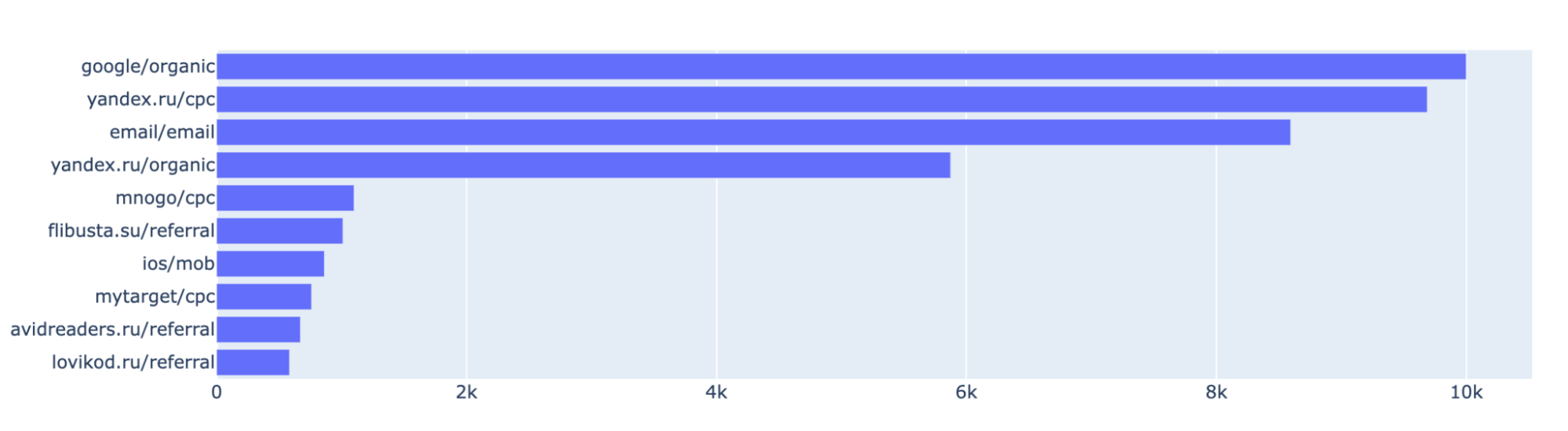
На графике отображается один столбец для каждого канала из топ-10, а высота столбца соответствует значению рейтинга этого канала. Каналы представлены на вертикальной оси, а рейтинг – на горизонтальной оси. Таким образом, чем выше значение рейтинга канала, тем длиннее столбец, соответствующий этому каналу.

Такая визуализация позволяет наглядно увидеть относительную важность различных каналов и сравнить их вклад в конверсию.

Атрибуция выручки на основе полученной оценки

После оценки вклада каждого канала в конверсию с помощью Марковских цепей, мы можем также атрибутировать выручку на основе полученных результатов. Это позволит нам увидеть, какой процент выручки приходится на каждый канал.

Сначала мы присваиваем вес каждой сессии на основе рейтинга канала, к которому эта сессия принадлежит:

test['weight'] = test['node'].apply(lambda x: res_dict[x])

Затем мы создаем функцию `attribute_revenue`, которая будет атрибутировать выручку каждому каналу на основе полученных весов. В этой функции мы выполняем следующие шаги:
1. Считаем общую выручку для каждой цепочки покупок с помощью группировки данных по клиентам и транзакционным группам:

df['chain_revenue'] = df.groupby(['clientId', 'transaction_group'])['cur_revenue'].transform(sum)

2. Оставляем только те строки, где общая выручка по цепочке больше 0:

df = df[df['chain_revenue'] > 0]

3. Рассчитываем долю каждой сессии в цепочке на основе ее веса и суммарного веса всех сессий в цепочке:

df['share'] = df['weight'] / df.groupby(['clientId', 'transaction_group'])['weight'].transform(sum)

4. Рассчитываем долю выручки для каждой сессии, умножая долю сессии на общую выручку цепочки:

df['revenue_share'] = df['share'] * df['chain_revenue']

5. Удаляем колонку с общей выручкой цепочки, так как она больше не нужна:

df.drop(columns=['chain_revenue'], inplace=True)

После применения функции `attribute_revenue` к нашим данным, мы группируем результаты по каналам и суммируем доли выручки для каждого канала. Затем делим сумму долей выручки на общую выручку, чтобы получить атрибуцию выручки для каждого канала:

markov_attrib = attribute_revenue(test).groupby('node')['revenue_share'].sum().sort_values() / test['cur_revenue'].sum()
markov_attrib = markov_attrib.rename('Цепи Маркова')

Теперь у нас есть атрибуция выручки для каждого канала на основе Марковских цепей, которую можно использовать для анализа и оптимизации маркетинговых стратегий.

Сравнение разных моделей атрибуции

На столбчатом графике, где по оси X будут отложены 5 комбинаций источник/канал, а по оси Y доля этих комбинаций в выручке для моделей (цепи Маркова, First touch, Last touch) и доля конверсий, можно увидеть различия в оценке эффективности каналов для разных моделей атрибуции (см. Рисунок 9).

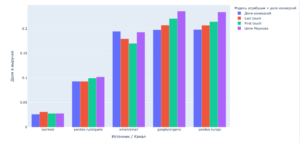
Например, можно заметить, что в таких каналах, как ’email/email’, ‘google/organic’ и ‘yandex.ru/cpc’, размер выручки значительно зависит от используемой модели атрибуции. Также нередки случаи, когда величина выручки канала ± совпадает для любой выбранной модели атрибуции.

Однако, стоит отметить, что анализируемый датасет в статье состоит из 13 миллионов сессий. Размер датасета может существенно влиять на результаты сравнения различных моделей атрибуции. Чем меньше база данных, которая будет анализироваться, тем вероятнее, что вы получите больше отличий при сравнении разных моделей атрибуции.

Это связано с несколькими факторами:

1. Больший размер датасета обеспечивает более точные и надежные результаты, так как он представляет собой более полное представление о поведении пользователей на сайте. С меньшим датасетом могут возникнуть проблемы с точностью и стабильностью результатов.
2. Меньшие датасеты могут быть подвержены смещениям из-за случайных колебаний или аномалий в данных. Это может привести к искажению результатов при сравнении различных моделей атрибуции.
3. Разные модели атрибуции могут быть более или менее чувствительными к размеру датасета. Например, модель атрибуции на основе Марковских цепей может быть более устойчивой к изменениям размера датасета, поскольку она учитывает все возможные пути пользователей и учитывает динамику взаимодействия между каналами.

Также, сравнивая различные модели атрибуции, мы можем заметить, что модель атрибуции на основе цепей Маркова может значительно отличаться от моделей типа First touch и Last touch. Вот несколько причин, по которым Марковская модель атрибуции отличается от других подходов:

1. Учитывает всю последовательность взаимодействия пользователя с каналами: Марковская модель атрибуции анализирует все шаги в пути пользователя от начала до конверсии, в отличие от моделей First touch и Last touch, которые приписывают весь успех лишь первому или последнему каналу соответственно.
2. Учитывает силу связей между каналами: Марковская модель атрибуции распределяет значение между каналами на основе их вероятностей перехода, что позволяет учесть взаимодействия между каналами и определить наиболее влиятельные комбинации.
3. Более гибкая и адаптивная: Марковская модель атрибуции может быть легко адаптирована к изменениям в поведении пользователей и маркетинговым стратегиям, в то время как другие модели могут быть слишком жесткими и ограниченными.
4. Устойчива к шуму: Модель атрибуции на основе цепей Маркова является более устойчивой к шуму и выбросам, поскольку она учитывает статистические закономерности в данных, а не просто присваивает значения на основе индивидуальных сессий.

Используя атрибутивные модели на основе цепей Маркова, компании имеют возможность идентифицировать самые прибыльные источники трафика и понять, какие каналы максимально способствуют увеличению дохода. Это знание призвано помочь бизнесу принимать обоснованные решения относительно того, какие маркетинговые стратегии и каналы следует приоритизировать, и на что, возможно, стоит перераспределить больше ресурсов и инвестиций.

Атрибутивные модели на основе Марковских процессов предлагают более точную и объективную оценку вклада каждого канала в конечные продажи. Благодаря этому можно более эффективно управлять маркетинговыми бюджетами, что в итоге приводит к улучшению показателей отдачи от инвестиций (ROI).

Таким образом, модели атрибуции, основанные на цепях Маркова, представляют собой мощный инструмент для маркетологов и аналитиков. С их помощью можно определить наиболее эффективные источники трафика, выявить возможности для оптимизации маркетинговых кампаний и увеличения доходности инвестиций.

Заключение

В нашем путешествии в мир Цепей Маркова мы увидели, как эти математические модели могут быть применены в сфере маркетинга для атрибуции. Мы прошли все этапы от понимания основных концепций и принципов работы Цепей Маркова до применения их на практике в реальных датасетах.

Мы увидели, как метод Цепей Маркова может обнаружить скрытые взаимосвязи в потоке данных о пользовательских сессиях и с уверенностью оценить вклад каждого канала в конечные продажи. Это позволяет нам принимать более обоснованные решения о распределении маркетинговых бюджетов и повышении эффективности маркетинговых кампаний.

Мы также обсудили эффект удаления и то, как его использование помогает нам улучшить качество атрибуции и сделать ее более точной. Подход с использованием Цепей Маркова позволяет нам не только оценить вклад отдельных каналов, но и увидеть, как меняется эта оценка при исключении одного или нескольких каналов.

Тем не менее, не стоит забывать о недостатках и ограничениях данного подхода. Цепи Маркова предполагают, что следующее состояние зависит только от текущего, и не учитывают более долгосрочные взаимосвязи. Это может быть проблемой при анализе данных, где присутствуют такие зависимости. Также, Цепи Маркова могут быть сложны для понимания и интерпретации, особенно для тех, кто только начинает свой путь в области аналитики.

В заключение хочется сказать, что Цепи Маркова — это мощный инструмент для анализа данных, который может предложить уникальные и полезные инсайты. Они могут помочь нам улучшить наши маркетинговые стратегии и повысить ROI, но они не являются панацеей и должны использоваться с осторожностью и пониманием их ограничений.