Аннотация
В эпоху мобильного интернета, сервис онлайн-заказа еды (OFOS) становится неотъемлемым компонентом инклюзивных финансов благодаря удобству, которое он приносит людям. Платформы OFOS предлагают динамическое распределение стимулов пользователей и продавцов через различные маркетинговые кампании для поощрения платежей, при этом сохраняя бюджетную эффективность платформ. Несмотря на значительный прогресс, сфера маркетинга продолжает сталкиваться с двумя основными вызовами:
(1) как распределить ограниченный бюджет с большей эффективностью, требующей точности в прогнозировании монотонной реакции пользователей, (т.н. чувствительности) на стимулы, и
(2) обеспечить пространственно-временную адаптивность и надёжность в различных маркетинговых кампаниях разного времени и места проведения.
В ответ на эти запросы мы предлагаем метод Ограниченной Монотонной Адаптивной Сети (CoMAN), подразумевающий пространственно-временное восприятие в рамках маркетингового бюджета. Конкретно, мы рассматриваем пространственно-временные предпочтения пользователей в пределах атрибута посредством двух основных модулей восприятия. Для дальнейшего повышения точности захвата изменений в чувствительности пользователей к стимулам в зависимости от времени и места, мы разрабатываем модули для изучения конвексности и конкавности и для выражения функций чувствительности. CoMAN может помочь в более эффективном распределении инклюзивных инвестиций в процессе ценообразования, что приведет к росту конверсии и заказов при сохранении эффективности бюджета. Большое количество результатов офлайн и онлайн экспериментов в рамках наших разнообразных маркетинговых кампаний демонстрируют эффективность предлагаемого подхода, превосходя классический монотонный метод, являющийся на сегодняшний день передовым.
Концепции системы классификации вычислений (CCS)
Информационные системы – Геолокационные услуги (LBS)
1 Введение
Посредством мобильных платежных сервисов, платформы OFOS, такие как Ele.me, Meituan и Uber Eats стали критически значимым компонентом в инклюзивном финансировании за счет удобства предоставления услуг в режиме реального времени. Платформы предлагают пользователям различные льготы (купоны, бонусы, скидки и пр.) посредством разнообразных маркетинговых стратегий и кампаний для стимулирования мобильных платежей в сфере питания и розничных поставок. Внутри этих маркетинговых кампаний критическим аспектом для платформы в повышении эффективности является разумное распределение стимулов потребителей и продавцов.
Пользователи демонстрируют разные модели отклика на стимулы платформы в зависимости от кампании. В общем смысле, коэффициент конверсии (CVR) выражает монотонно растущую тенденцию с пакетами скидок и суммарными скидками, в то время как она же снижается при достижении порога имеющихся купонов. По аналогии мы видим монотонно убывающую зависимость от стоимости доставки.
Предыдущая наша работа в сфере маркетинга исследовала разные методы оптимизации стимулов при ограниченном бюджете. Подход к ценообразованию в маркетинге основан на использовании парадигмы, состоящей из двух компонентов: прогнозирование оценок откликов пользователей и принятие решений в режиме реального времени посредством линейного программирования. Важно, что в сфере доставки еды, где предпочтения пользователей напрямую зависят от пространственно-временных факторов, соответствующие исследования изучали и и расширяли информацию о пространственно-временных условиях.
Однако, все предыдущие исследования в области маркетинга доставки еды не учитывают критическую важность пространственно-временного восприятия, сосредотачиваясь на анализе чувствительности пользователей к различным стимулам в общем контексте. На самом деле, чувствительность пользователей меняется также в зависимости от того, к какому продавцу они обращаются, когда и в каком месте. Полагаться на единый функционал чувствительности пользователя в оценке откликов не является корректным. Таким образом, предлагаемая модель обладает улучшенной точностью прогнозирования и надежностью адаптации к разнообразным маркетинговым стратегиям.
В этой статье мы решаем эти проблемы опираясь на Ограниченную монотонную адаптивную сеть (CoMAN) – новую маркетинговую модель ценообразования, в основе которой лежит пространственно-временной монотонный отклик. Конкретно наш метод использует два пространственно-временных модуля активации для руководства всей модели в обучении и понимании пространственно-временных факторов, что облегчает и делает более рациональной информацию, получаемую о восприятии пространства и времени. Кроме того, наш тщательно разработанный монотонный слой улучшает восприятие пространственно-временной дифференциации в монотонных откликах пользователей на стимулы. Одновременно мы вводим функцию активации, адаптированную для адаптивного изучения функции чувствительности пользователей к стимулам в маркетинговой сфере. В конечном итоге, CoMAN достигает строгого, непрерывного, монотонного, точного и плавного приближения функции чувствительности к стимулам в различных пространственно-временных измерениях. Эффективность предлагаемой методологии демонстрируется через обширные онлайн и офлайн эксперименты в рамках разнообразных маркетинговых кампаний. Вкратце, наши основные достижения следующие:
- Мы выделяем основные проблемы, с которыми можно столкнуться в области маркетинга, и анализируем значимость осведомленности о пространственно-временных предпочтениях, а также разрабатываем новую модель для решения этих вопросов. Насколько нам известно, наша модель является первой, систематически моделирующей монотонный отклик, воспринимая пространственно-временную информацию в разнообразии сферы доставки еды.
- Мы предлагаем монотонный слой, который использует восприятие пространственно-временной информации для улучшения моделирования монотонных откликов. Этот модуль адаптивно изучает конвексность, конкавность и параметрическое выражение функций чувствительности к стимулам пользователей в различных маркетинговых кампаниях, обусловленных различными пространственно-временными характеристиками.
- Мы разрабатываем строго монотонную активационную функцию Convex Linear Unit (CLU), адаптированную для различных маркетинговых задач. Мы используем эту активационную функцию для гибкого изучения различий в выражениях монотонных функций. Мы демонстрируем, что эта строго выпуклая функция способна более точно моделировать функции отклика пользователей на стимулы.
2 Связанные работы
Функции активации. Функции активации играют ключевую роль в нейронных сетях, вводя нелинейные преобразования, что позволяет глубоким моделям улавливать сложные шаблоны, недоступные для линейных операций. Ряд исследований разработали варианты функции ReLU, которые смягчают эту проблему, разрешая небольшой, ненулевой градиент в качечестве отрицательного фактора, что позволило улучшить производительность модели. Ряд работ исследовали, как комбинировать выходные данные оригинального ReLU с его точечным отражением в пределах одного и того же слоя нейронной сети.
Монотонность архитектуры. Методы исследования моделирования монотонного отклика можно разделить на два основных типа. Первый включает конструкцию монотонной структуры, такую как ограничение веса сети исключительно неотрицательными или неположительными значениями, что гарантирует, что модель будет демонстрировать либо монотонно возрастающее, либо монотонно убывающее поведение. Другой метод использует регуляризацию для наложения монотонности, сети реализуют монотонность через модифицированные функции потерь или эвристические регуляризационные термы во время обучения. Min-Max сети используют монотонное линейное встраивание и max-min-пулинг, чтобы наделить сети широкими моделирующими возможностями, но их сложно тренировать и применять на практике. Глубокая решетчатая сеть (DLN) применяет ограничения к парам параметров решетки, но ограничивает пространство аппроксимации функций и требует значительного количества изучаемых параметров. CMNN может аппроксимировать любую непрерывную монотонную функцию, комбинируя ненасыщенные и насыщенные функции активации, но не обладает способностью к адаптивному обучению.
Монотонность через регуляризацию. Как упоминалось выше, обеспечение монотонности во время обучения также может быть достигнуто путем модификации функции потерь или включения регуляризационных терминов. А. Сивараман и др. представили механизм, основанный на решателях Satisfiability Modulo Theories (SMT), способных идентифицировать пары точек, нарушающих монотонные ограничения (т.е. контрпримеры). Лю и др. преобразуют математическую проверку монотонности на произвольных кусочно-линейных (т.е. ReLU) сетях в задачу смешанного целочисленного линейного программирования (MILP), которая может быть эффективно решена с помощью существующих решателей MILP. Оба метода, MILP и SMT, зависят от кусочно-линейного свойства ReLU для проверки ограниченного монотонного обучения, но не могут быть расширены на другие функции активации, такие как ELU, SELU, GELU и т.д. Более того, вычислительные затраты, связанные с этими техниками, значительны и часто требуют множества итераций для достижения строго проверенной монотонной модели.
3 Подготовительный этап
Мы формулируем маркетинговую проблему как проблему линейного программирования, решаемую оптимизацией. Набор пользователей мы определяем как С, набор кандидатов на значения стимулов как Т, где 𝑡𝑗 ∈ T представляет собой 𝑗-ое воздействие. Наша цель – найти стратегию распределения стимулов, которая позволит оптимально распределить стимулы для максимизации прибыли от отклика пользователей (т.н. CVR) в рамках границ бюджета В. Вид формулы:
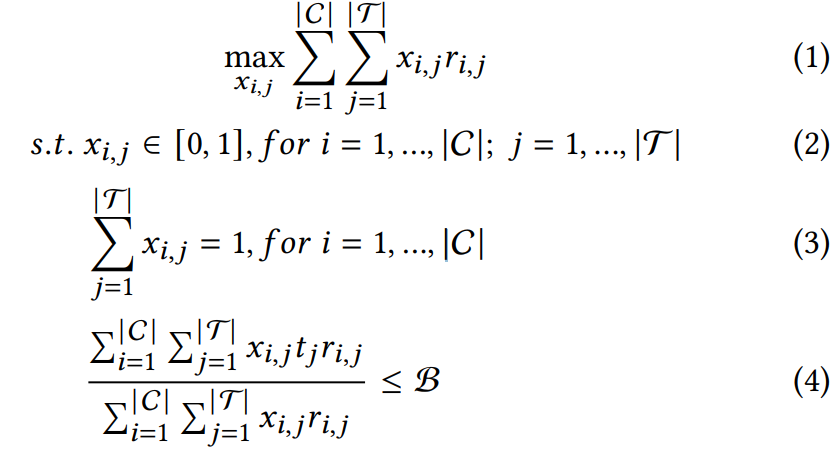
где 𝑥>𝑖,𝑗 обозначает вектор решений, указывающий, было ли воздействие 𝑡𝑗 назначено пользователю 𝑖, а 𝑟𝑖,𝑗 представляет собой оценку отклика по нашей модели отклика. А ![]() является значением стимула для пользователя в рамках ограничения 3. Более того, ограничение в уравнении 4 указывает на ограниченное среднее значение стимула для каждого пользователя. Вводя двойственные переменные 𝜇𝑖 и 𝜆, соответствующие вышеупомянутым ограничениям 3 и 4, мы преобразуем исходную задачу в её двойственную форму. Выпуклая задача оптимизации, описанная в целевой функции 1, решается с применением метода множителей Лагранжа, формально представленного следующим образом:
является значением стимула для пользователя в рамках ограничения 3. Более того, ограничение в уравнении 4 указывает на ограниченное среднее значение стимула для каждого пользователя. Вводя двойственные переменные 𝜇𝑖 и 𝜆, соответствующие вышеупомянутым ограничениям 3 и 4, мы преобразуем исходную задачу в её двойственную форму. Выпуклая задача оптимизации, описанная в целевой функции 1, решается с применением метода множителей Лагранжа, формально представленного следующим образом:
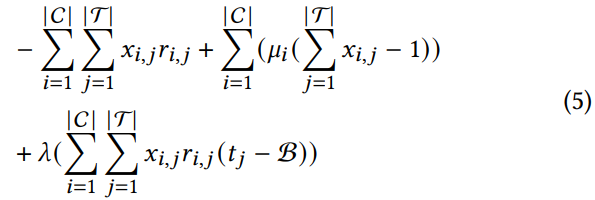
Изменив уравнение 5, получаем:
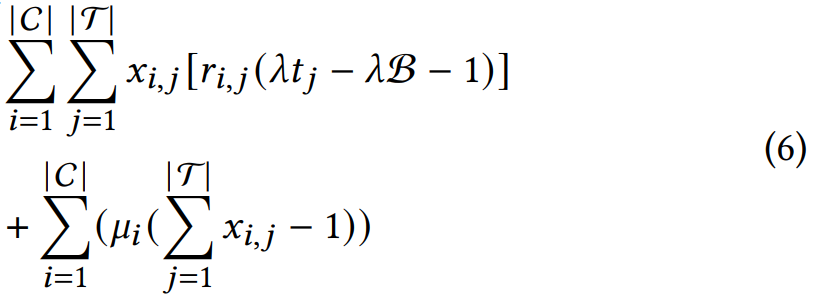
Учитывая, что как целевая функция, так и функции ограничений являются выпуклыми, оптимальное значение 𝜆∗ получается путем применения условий Каруша-Куна-Таккера (KKT) и метода L-BFGS. Из уравнения 6 можно заметить, что различные значения стимулов связаны только с первым членом. Следовательно, приближенное решение может быть получено следующим образом:
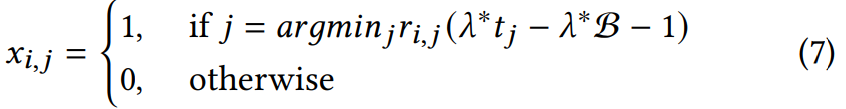
При принятии решений о ценообразовании в режиме онлайн мы используем нашу модель отклика для предсказания оценок отклика |T| раз на основе кандидатов для каждого запроса. Затем, используя вычисленное в реальном времени значение 𝜆∗ вместе с уравнением принятия решений 7, чтобы определить значение стимула.
4 Методы
В маркетинговых кампаниях мы разработали многозадачную модель в качестве модели ценообразования, предсказывающую различные бизнес-цели, такие как коэффициент конверсии (CVR) или CTCVR (коэффициент кликов и конверсий) и валовый объем продаж (GMV). Учитывая, что предсказания задач не имеют существенной взаимосвязи, существует риск столкнуться с феноменом качелей (Seesaw Phenomenon) при обучении многозадачной модели. Это может привести к улучшению одной задачи в ущерб другой. Чтобы смягчить этот эффект, мы используем многозадачную структуру Progressive Layered Extraction (PLE) и предлагаем ограниченную монотонную адаптивную сеть (CoMAN).
Обзор. Дизайн и моделирование предлагаемой нами структуры сосредоточены на трех критически важных аспектах: активация пространственно-временных корреляций в атрибутивных признаках, моделирование монотонного отклика на стимулы в различных маркетинговых кампаниях и повышение адаптивности модели к пространственно-временным различиям в монотонном слое. Общая архитектура представлена на Рисунке 1.
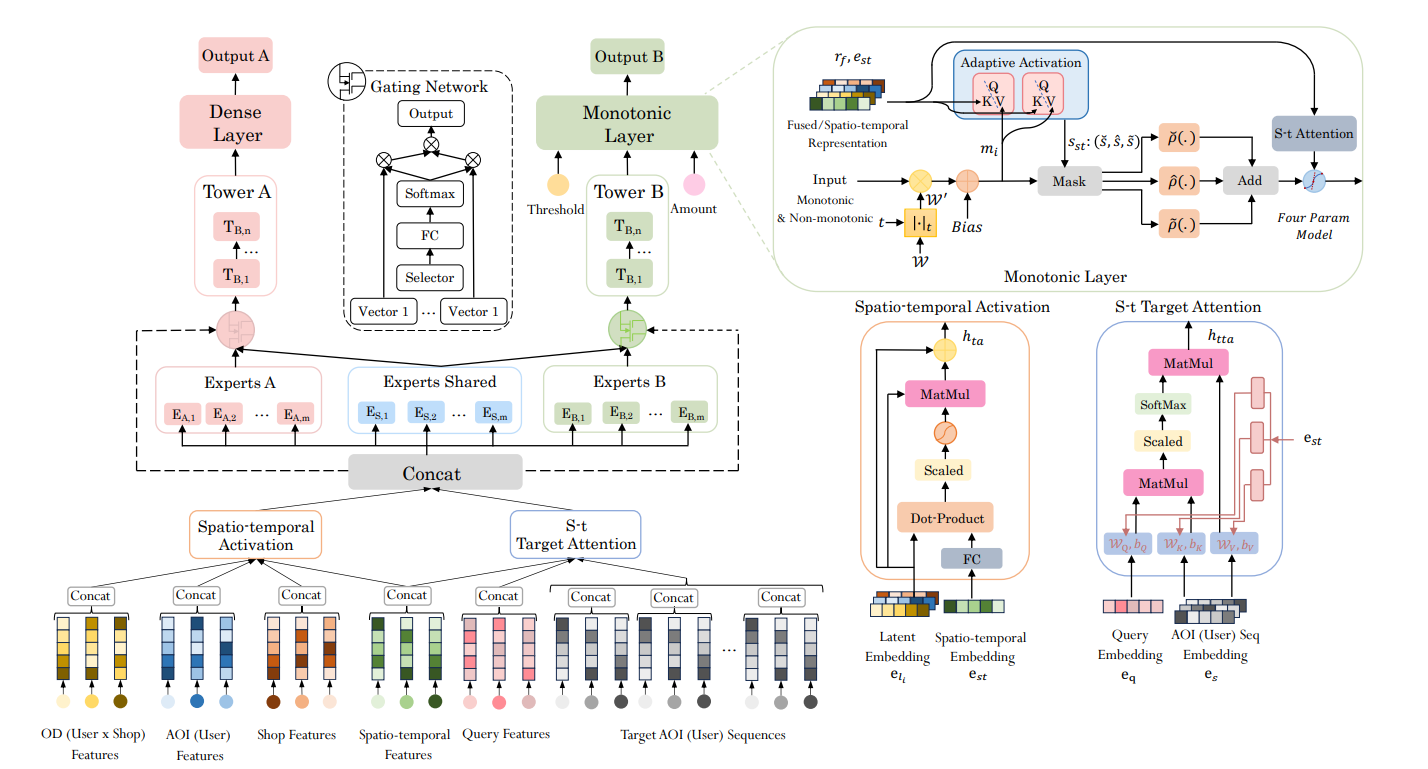
В процессе извлечения признаков мы делим период на пять интервалов: завтрак (04:00–10:00), обед (10:00–14:00), полдник (14:00–17:00), ужин (17:00–20:00) и ночной перекус (20:00–04:00), и собираем числовые признаки для каждого периода. Мы создаем временные признаки, включая информацию, такую как григорианские и лунные даты, праздники и дни недели для каждого дня. Одновременно мы формируем пространственные признаки из географических данных, охватывающих текущее местоположение пользователя, идентификатор города, идентификатор района и идентификатор AOI (зона интереса). Примечательно, что в некоторых маркетинговых кампаниях, отличающихся от моделирования на уровне пользователей, мы применяем региональное моделирование для AOI. Таким образом, в зависимости от маркетинговых кампаний, мы адаптируем наши признаки для использования либо пользователей, либо AOI (например, перекрестные признаки, исторические последовательности кликов).
Активация пространственно-временной корреляции. В модуле временной активации пространственно-временные признаки используются для вычисления весов каждого встраивания признаков (например, Пользователь, Магазин, Запрос) 𝑒𝑙𝑖 через операцию скалярного произведения, за которой следует сигмоидная функция. Этот процесс направлен на захват динамических вариаций, присущих пространственно-временным представлениям. Полученный результат затем умножается на входные представления и интегрируется через остаточное соединение, предназначенное для активации пространственно-временной информации, заключенной в встраиваниях признаков. Выход модуля временной активации, обозначаемый как ℎ𝑡𝑎, можно сформулировать следующим образом:
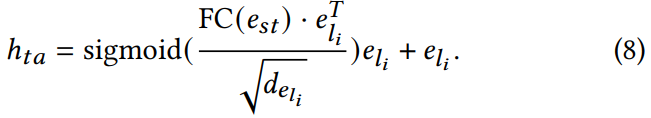
Используется механизм временного целевого внимания для выявления предпочтений интересов различных AOI/пользователей к магазинам, одновременно эффективно изучаются вариации в разных временных и пространственных рамках. Мы достигаем этого путем линейной проекции векторов Запроса, Ключа и Значения с весами и смещением (например, [𝑤𝑄, 𝑏𝑄]), которые генерируются полностью связанной нейронной сетью соответственно. Выход модуля, обозначаемый как ℎ𝑡𝑡𝑎, формулируется следующим образом:
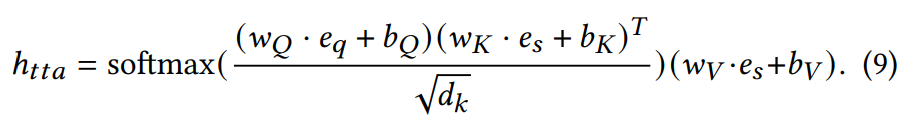
Монотонный отклик. Чтобы обойти трудности в обучении при сочетании традиционных линейных монотонных ограничений с насыщенными (ограниченными) активационными функциями и ограничения, связанные с тем, что только выпуклые модели могут быть обучены при использовании выпуклых активационных функций, мы создаем монотонный слой на основе структуры ограниченных монотонных нейронных сетей (CMNN). Этот подход не только облегчает использование ненасыщенных активационных функций, но и позволяет априори моделировать различные степени выпуклости и вогнутости в различных сценариях применения.
Мы используем вектор индикатора монотонности 𝑡 ∈ {−1, 0, 1}𝑛 для поэлементного преобразования весов вектора признаков с целью ограничения монотонности. Операция | · |𝑡 применяется следующим образом:
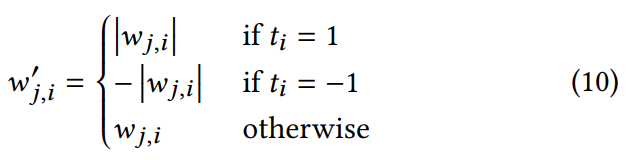
Мы строго определяем выпуклую активационную функцию 𝜌˘ ∈ A˘, где A˘ обозначает множество всех выпуклых, монотонно возрастающих, ограниченных снизу, центрированных в нуле функций. А также мы определяем вогнутую активационную функцию 𝜌ˆ(𝑥) и насыщенную активационную функцию 𝜌˜(𝑥) следующим образом:
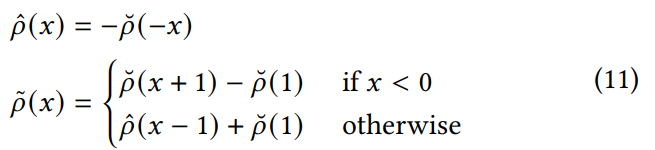
Функция 𝜌ˆ(𝑥) является вогнутой и ограниченной сверху, в то время как функция 𝜌˜(𝑥) является насыщенной и ограниченной. Кроме того, вводится вектор выбора активации s = (𝑠˘, 𝑠ˆ, 𝑠˜) ∈ N3, и 𝑠˘ + 𝑠ˆ + 𝑠˜ = 𝑚, чтобы приблизить вогнутость и выпуклость монотонного отклика путем комбинирования вогнутых, выпуклых и насыщенных активационных функций, где 𝑚 обозначает размерность монотонных переменных. В частности, установив s = (𝑚, 0, 0), мы гарантируем, что монотонный отклик моделируется как выпуклая функция, с аналогичными принципами, применяемыми для вогнутого моделирования. Затем выход комбинированных активационных функций 𝜌s применяется поэлементно следующим образом:
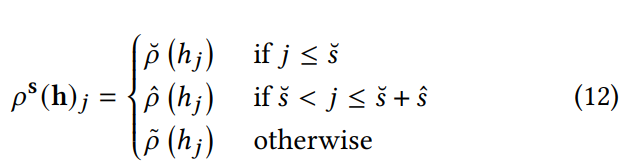
В то же время, чтобы гибко адаптироваться к разнообразным пространственно-временным свойствам маркетинговых кампаний и изучать монотонные функции отклика, мы вводим строго монотонную выпуклую функцию активации, названную Выпуклая Линейная Единица (Convex Linear Unit, CLU). Более того, мы выводим соответствующую вогнутую функцию активации 𝜌ˆ(𝑥) и насыщенную функцию активации 𝜌˜(𝑥) через CLU. Конструкция функций активации показана на Рисунке 3, с математическими выражениями CLU следующим образом:
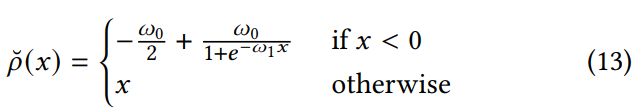
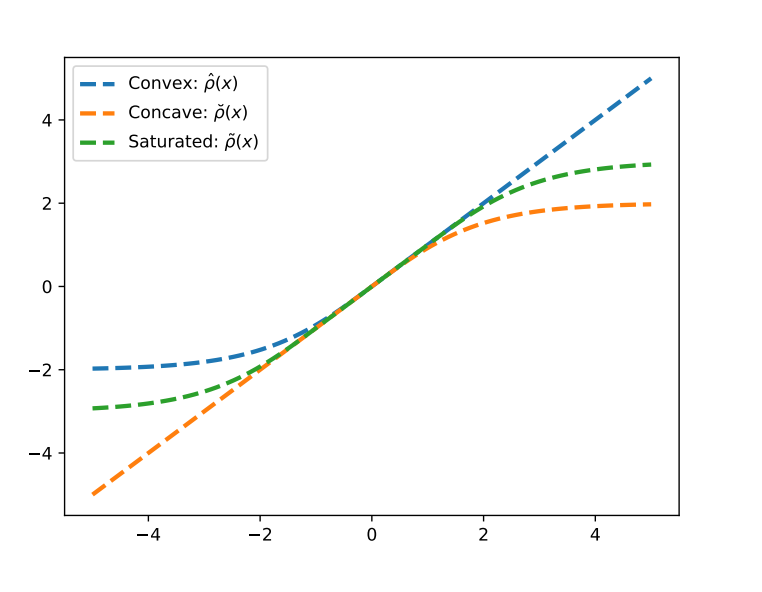
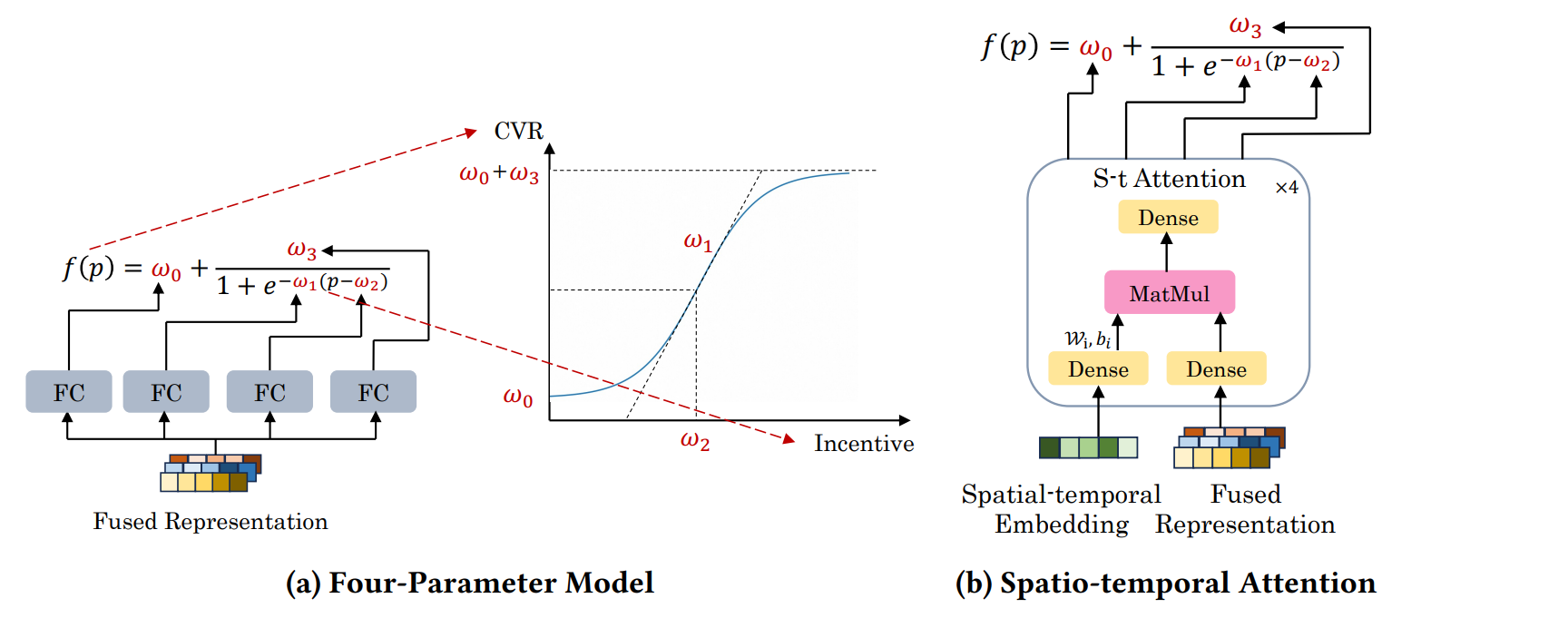
Теорема универсальной аппроксимации утверждает, что любая непрерывная функция на замкнутом интервале может быть аппроксимирована нейронными сетями с неполиномиальными функциями активации. В то же время, любая многомерная непрерывная монотонная функция на компактных подмножествах R𝑘 может быть аппроксимирована монотонно ограниченными нейронными сетями с не более чем 𝑘 скрытыми слоями, используя сигмоидную активацию. Вдохновленные этим, мы предлагаем Модель с Четырьмя Параметрами (Four-Parameter Model, FPM) через адаптивное преобразование сигмоидной функции, в сочетании с CMNN (Constrained Monotonic Neural Network) структурой, чтобы гибко аппроксимировать монотонные функции отклика в сложных сценариях.
Рисунок 2a поясняет функциональную форму и параметрическое поведение метода FPM. Мы изучаем и интерпретируем кривую чувствительности к стимулам через четыре параметра, каждый из которых имеет ощутимое значение в маркетинге. Параметр 𝜔0 представляет естественный уровень конверсии при отсутствии каких-либо стимулов со стороны платформы. Параметр 𝜔1 обозначает чувствительность пользователя в точке мотивационного перегиба 𝜔2, в то время как 𝜔3 соответствует максимальному уровню конверсии, достижимому пользователем.
Усиление адаптивного отклика. Чтобы позволить модели изучать изменчивость монотонного отклика в различных пространственно-временных измерениях, мы разработали модули адаптивной активации и пространственно-временного внимания (S-t Attention) в рамках монотонного слоя для повышения способности модели воспринимать пространственно-временную информацию. Эти модули предназначены для гибкой адаптации выпуклости, вогнутости и параметрических выражений функций монотонного отклика через пространственно-временные представления.
В предыдущей методологии CMNN параметр s является априорным и требует ручной настройки, а не позволяет адаптивное обучаться. Точка перегиба функции монотонного отклика делит её на выпуклые и вогнутые сегменты. Основываясь на этих инсайтах, мы предлагаем модуль адаптивной активации, способный адаптивно изучать и регулировать пропорцию выпуклости и вогнутости, улавливая и объединяя глубокие представления с пространственно-временной информацией. Как показано слева от монотонного слоя на Рисунке 1, мы маскируем различные части монотонного представления 𝑚𝑖 с адаптивно изученным коэффициентом соотношения выпуклости-вогнутости 𝑠𝑠𝑡, а затем комбинируем их через выпуклые, вогнутые и насыщенные функции активации отдельно. Операции адаптивной активации можно объяснить следующим образом:
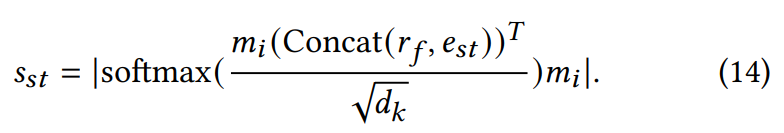
Мы разработали модуль пространственно-временного (S-t) внимания для использования пространственно-временной информации с целью дальнейшей адаптивной настройки и обучения FPM. Во-первых, мы генерируем веса и смещения ([𝑤𝑖, 𝑏𝑖]) для векторов глубоких объединенных представлений (например, пользователей, магазинов и т.д.) через полностью связанный слой. Затем мы проводим вычисления матричного умножения для получения параметров FPM. Структура модуля показана на Рисунке 2b и может быть сформулирована следующим образом:
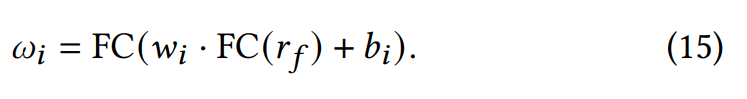
5 Испытания
5.1 Настройка эксперимента
Описание набора данных. Мы провели эксперименты на реальных наборах данных из двух маркетинговых кампаний на платформе Ele.me, одной из крупнейших платформ онлайн-заказа в Китае. Обучающие наборы данных охватывают одну неделю, в то время как тестовый набор данных охватывает один день. Примечательно, что мы случайным образом выбрали 5% онлайн-трафика в качестве детектируемого трафика для случайного распределения значений стимулов, которые служат эталоном для аппроксимации функции чувствительности к стимулам.
- Набор данных «Взрывные красные пакеты» (прим.: в контексте цифрового маркетинга, в Китае в частности, «взрывные красные пакеты» представляют собой виртуальные подарки или бонусы, которые пользователи могут получить при выполнении определенных действий, таких как совершение покупок, участие в акциях или выполнении заданий, концепция основывается на древнекитайской традиции дарения красных конвертов с деньгами) Ежедневно отправляется в среднем 10 миллионов взрывных красных пакетов пользователям онлайн. Это классификационный набор данных с примерно 1,05 миллионами ежедневных обучающих образцов и почти 400 признаками, в конечном итоге достигается 8,4 миллиона образцов. Для оценки точности предсказания функций чувствительности мы обучали модели, используя несмещенные образцы, собранные из онлайн детектируемого трафика.
- Набор данных «Освобождение от платы за доставку»: Это регрессионный набор данных, охватывающий примерно 3,2 миллиона AOI (областей интереса), с около 4,3 миллионами магазинов и 303 признаками. Ежедневные образцы составляют около 770 миллионов, а общий объем превышает 6 миллиардов образцов.
Базовые модели. Для проверки эффективности предлагаемой нами методологии мы сравниваем её с несколькими передовыми методами, используемыми в качестве базовых моделей:
- a) DNN: Это наивная модель, лишённая возможностей пространственно-временного и монотонного моделирования.
- b) DNN-M: Этот метод ограничивает веса нейронной сети исключительно неотрицательными или неположительными значениями и использует сигмоидные функции активации для монотонного моделирования.
- c) FPM: Этот подход использует математическую четырёхпараметрическую функцию для независимого приближения монотонной функции отклика.
- d) CMNN: Этот метод использует структуру CMNN в сочетании с различными базовыми выпуклыми функциями активации, включая CLU, предложенную в нашем исследовании, при этом комбинируя сигмоидную функцию в качестве конечной функции активации.
Гиперпараметры. В наших экспериментах для набора данных «Взрывные красные пакеты» размер батча при обучении модели установлен на 128, с использованием оптимизатора Adagrad и скоростью обучения 0.001. В наборе данных «Освобождение от платы за доставку» размер батча настроен на 1024, также с использованием оптимизатора Adagrad, но со скоростью обучения 0.012. Кроме того, все эксперименты проводятся на AOP4 с использованием 40 серверных параметров и 400 рабочих потоков.
5.2 Результаты испытаний
Исследование абляции. Для всестороннего понимания возможностей нашей предложенной модели CoMAN в аппроксимации функций чувствительности к стимулам, и признавая, что модули S-t внимания и адаптивной активации составляют основные компоненты модели CoMAN, мы провели исчерпывающие исследования абляции для оценки эффективности этих ключевых модулей. Соответственно, мы ввели три варианта абляции:
- a) CoMAN без (S-t и AA) (CoMAN-B), эта базовая версия использует CMNN на основе CLU в сочетании с FPM в качестве конечной функции активации.
- b) CoMAN без AA, эта версия исключает модуль адаптивной активации из модели CoMAN.
- c) CoMAN без S-t, этот вариант исключает модуль S-t внимания из структуры CoMAN.
Эти версии оцениваются по сравнению с полной моделью CoMAN, которая интегрирует все модули, чтобы систематически оценить влияние каждого модуля на общую производительность модели. В частности, сравнительные эксперименты CMNN без пространственно-временной активации и модулей пространственно-временного целевого внимания.
Таблица 1: Общая производительность на задачах «Взрывные красные пакеты» и «Освобождение от платы за доставку».
| Метод | Взрывные красные пакеты | Освобождение от платы за доставку | ||||||
| AUC↑ | MSE↓ | KL Div↓ | Corr Coeff↑ | MAE↓ | MSE↓ | KL Div↓ | Corr Coeff↑ | |
| DNN[29] | 0.6974 | 0.0636 | 0.6243 | 0.8513 | 0.1841 | 0.0831 | 0.8332 | 0.8304 |
| DNN-M[1] | 0.7022 | 0.0431 | 0.4259 | 0.8713 | 0.1232 | 0.0422 | 0.5347 | 0.8629 |
| FPM | 0.7113 | 0.0293 | 0.1901 | 0.9066 | 0.0913 | 0.0323 | 0.3083 | 0.8961 |
| CMNN[28](ReLU[23]) | 0.7111 | 0.0282 | 0.1848 | 0.9150 | 0.0894 | 0.0298 | 0.2772 | 0.8916 |
| CMMM(ELU[4]) | 0.7139 | 0.0273 | 0.1737 | 0.9171 | 0.0823 | 0.0281 | 0.2761 | 0.9127 |
| CMNN(CLU) | 0.7151 | 0.0269 | 0.1718 | 0.9189 | 0.0809 | 0.0274 | 0.2343 | 0.9143 |
| CoMAN-B | 0.7348 | 0.0224 | 0.1305 | 0.9229 | 0.0769 | 0.0263 | 0.2218 | 0.9193 |
| CoMAN без AA | 0.7414 | 0.0191 | 0.0984 | 0.9333 | 0.0624 | 0.0227 | 0.1897 | 0.9326 |
| CoMAN без S-t | 0.7407 | 0.0159 | 0.0925 | 0.9357 | 0.0733 | 0.0243 | 0.1809 | 0.9273 |
| CoMAN | 0.7480 | 0.0115 | 0.0901 | 0.9486 | 0.0454 | 0.0184 | 0.1211 | 0.9469 |
| +0.0506 | +0.0521 | +0.5342 | +0.0973 | +0.1387 | +0.0647 | +0.7121 | +0.1165 | |
Таблица 2: Оценка временных сегментов на задаче «Взрывающиеся красные пакеты». Мы обозначаем следующие периоды: Завтрак (Bkfst), Обед (Lch), Полдник (A.Tea), Ужин (Din) и Полуночный перекус (M.S.).
| Метод | MAE↓ | KL Div↓ | ||||||||||
| Bkfst | Lch | A.Tea | Din | M.S. | Общий | Bkfst | Lch | A.Tea | Din | M.S. | Общий | |
| FPM | 0.1782 | 0.1385 | 0.1461 | 0.1297 | 0.1118 | 0.1325 | 0.1395 | 0.0824 | 0.1024 | 0.0918 | 0.0439 | 0.2801 |
| CoMAN | 0.0369 | 0.0449 | 0.0529 | 0.0780 | 0.0629 | 0.0448 | 0.0297 | 0.0288 | 0.0432 | 0.0737 | 0.0360 | 0.1480 |
| +0.1413 | +0.0936 | +0.0932 | +0.0517 | +0.0489 | +0.0877 | +0.1098 | +0.0536 | +0.0592 | +0.0181 | +0.0079 | +0.1321 | |
Таблица 3: Оценка временных сегментов на задаче «Освобождение от платы за доставку».
| Метод | MAE↓ | KL Div↓ | ||||||||||
| Bkfst | Lch | A.Tea | Din | M.S. | Общий | Bkfst | Lch | A.Tea | Din | M.S. | Общий | |
| FPM | 0.1073 | 0.0883 | 0.1021 | 0.0932 | 0.0972 | 0.0943 | 0.0721 | 0.0809 | 0.0678 | 0.0733 | 0.0749 | 0.3692 |
| CoMAN | 0.0771 | 0.0569 | 0.0732 | 0.0631 | 0.0654 | 0.0632 | 0.0307 | 0.0276 | 0.0283 | 0.0259 | 0.0271 | 0.1398 |
| +0.0302 | +0.0314 | +0.0289 | +0.0301 | +0.0318 | +0.0311 | +0.0414 | +0.0533 | +0.0395 | +0.0474 | +0.0478 | +0.2294 | |
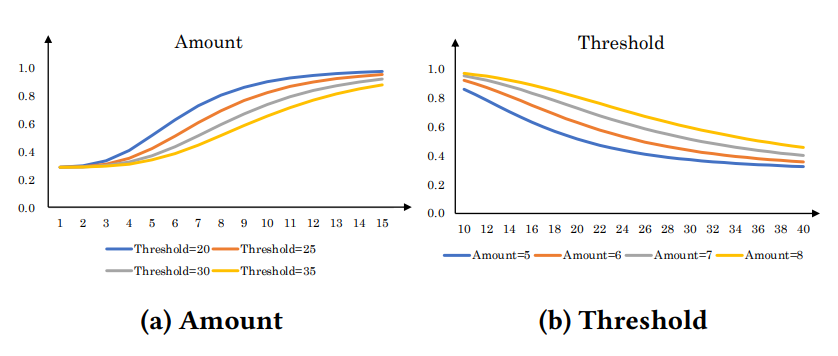
Кроме того, мы также используем структуру CMNN, чтобы продемонстрировать эффективность предложенной функции активации CLU в адаптивной настройке ответов на стимулы в различных маркетинговых кампаниях. Для проверки монотонного свойства отклика CoMAN мы проводим оффлайн-тесты, в которых все немонотонные характеристики остаются постоянными, в то время как монотонные характеристики (например, количество и порог) увеличиваются. Затем строим кривые монотонного отклика CVR, как показано на рисунках 4a и 4b соответственно. Для оценки нашей задачи монотонного моделирования мы представляем результаты монотонного слоя из оффлайн-экспериментов в таблице 1, в то время как таблица 2 и таблица 3 демонстрируют производительность модели во время онлайн-маркетинговых кампаний.
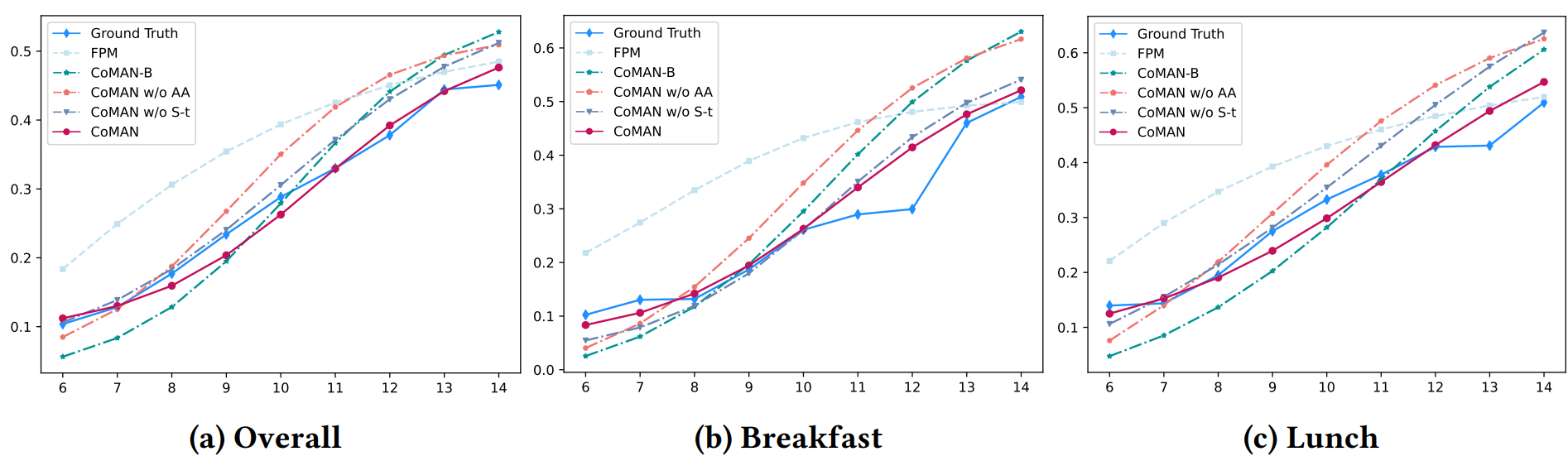
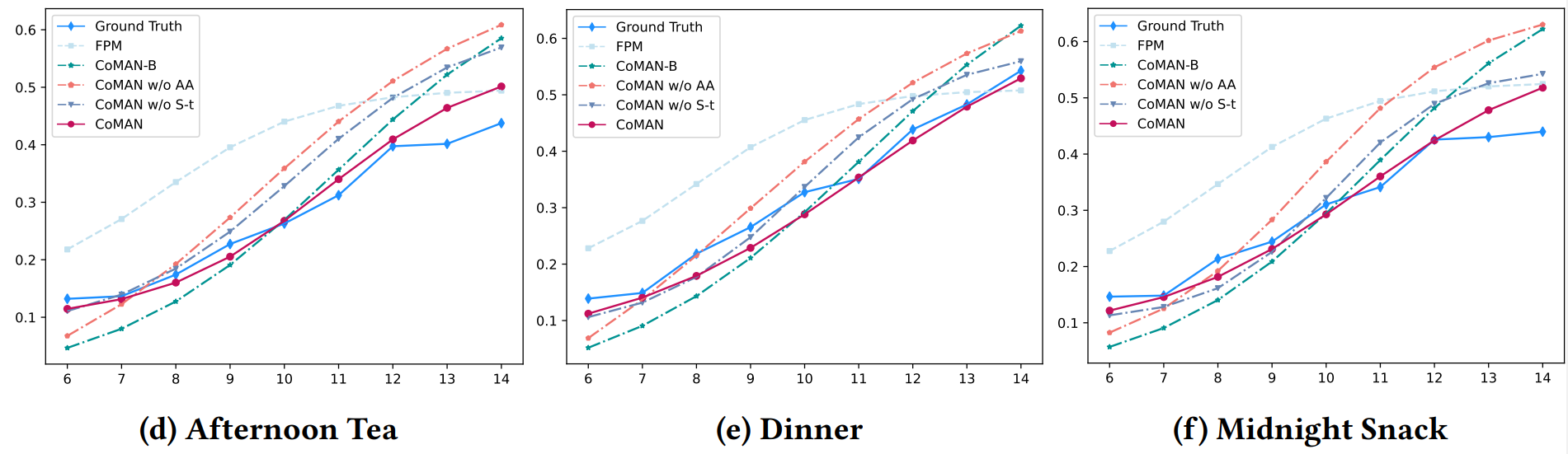
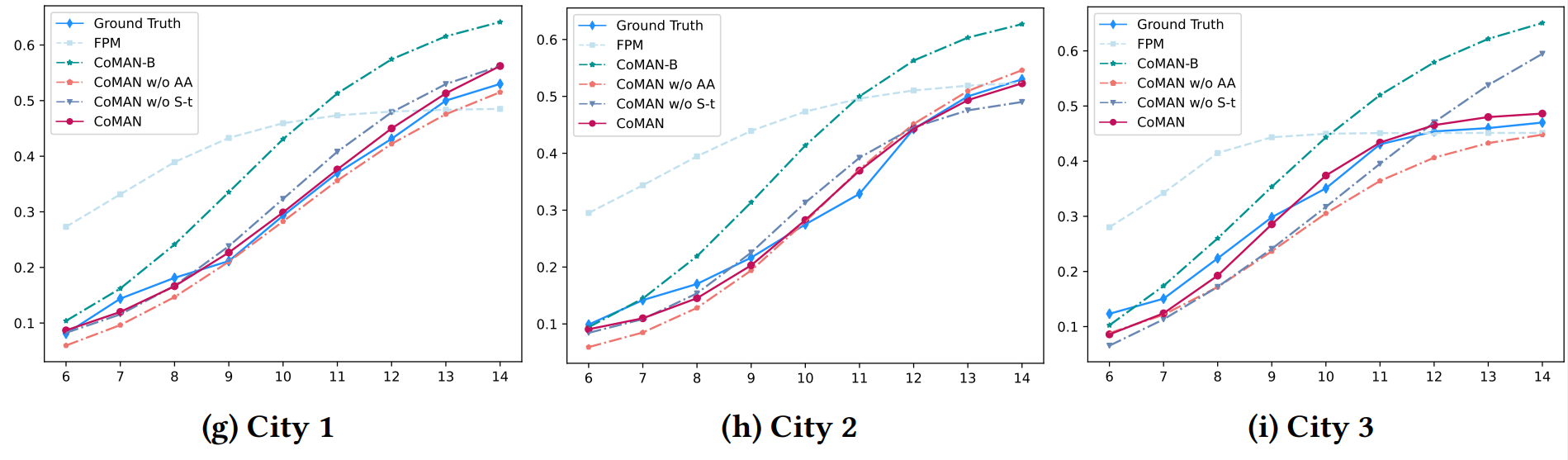
Результаты, представленные в вышеуказанных таблицах, показывают, что два модуля в монотонном слое модели CoMAN соответствуют нашим ожиданиям, достигая значительных улучшений как в точности, так и в прогнозировании реальных распределений. Это демонстрирует, что CoMAN может адаптивно настраивать выпуклость, вогнутость и выражение монотонных функций отклика в различных маркетинговых кампаниях, улучшая восприятие пространственно-временной информации. Более того, как показано на рисунке 5, мы оцениваем предсказанные моделью онлайн монотонные кривые отклика как в целом, так и в течение пяти периодов, а также для трех городов с наибольшим числом пользователей. Результаты подгонки как для усеченной, так и для полной версии CoMAN более точно приближаются к истинному распределению по сравнению с базовой моделью, что дополнительно подтверждает эффективное захватывание пространственно-временных характеристик CoMAN в реальных маркетинговых кампаниях.
Онлайн A/B тест. Мы внедрили нашу методологию на платформе Ele.me и провели двухнедельный онлайн A/B тест. По сравнению с базовой онлайн-моделью, наша предложенная модель приносит больше пользы, при этом сохраняя или даже снижая субсидии платформы, что помогает маркетинговому бизнесу улучшить эффективность бюджета и обеспечить больший рост. Подробные результаты онлайн-тестирования представлены в таблице 4.
Примечательно, что в рамках региональной стратегии ценообразования для маркетинговой кампании по отмене платы за доставку модель CoMAN также способствует значительным бизнес-выгодам для платформы. Это достигается даже при снижении интенсивности субсидий на 0,76%, что приводит к увеличению роста заказов на 0,70%, улучшению CTCVR на 0,62% и увеличению GMV на 1,06%.
Таблица 4: Метрики онлайн-эффективности бизнеса. По сравнению с методом онлайн FPM, модель CoMAN продемонстрировала улучшение показателей в маркетинге Ele.me.
| Модель | CVR | GMV | Заказы |
| CoMAN-B | +0.82% | +0.10% | +0.45% |
| CoMAN w/o AA | +1.20% | +0.51% | +1.56% |
| CoMAN w/o S-t | +2.18% | +3.02% | +3.57% |
| CoMAN | +3.09% | +3.63% | +3.68% |
6 Заключение
В данной статье мы предлагаем новую модель ограниченного монотонного отклика CoMAN для улучшения монотонного моделирования за счет адаптивного пространственно-временного восприятия в различных маркетинговых кампаниях по доставке еды. В частности, мы используем два модуля пространственно-временного восприятия для активации и захвата пространственно-временных характеристик в представлениях атрибутов. Затем, для монотонного слоя, мы разработали два модуля, которые используют пространственно-временную информацию для улучшения адаптивного обучения вогнутости и выпуклости, а также выражения функции чувствительности. Комплексное оффлайн и онлайн A/B тестирование, проведенное в рамках двух маркетинговых кампаний на платформе Ele.me, демонстрирует превосходство нашего предложенного подхода. В конечном итоге исследования доказывают, что наша модель более точно отражает чувствительность пользователей к стимулам в разных местах и периодах и демонстрирует превосходную ценовую производительность в различных пространственно-временных измерениях, тем самым достигая цели повышения эффективности маркетинга. Более того, в будущих исследованиях будет уделено внимание более тонкому определению различий в чувствительности пользователей к стимулам в различных пространственно-временных измерениях.